Back to Edexcel Probability (H) Home
Probability: Quiz 10
Probability: Quiz 10
Click here for a printout of the diagrams in this quiz.
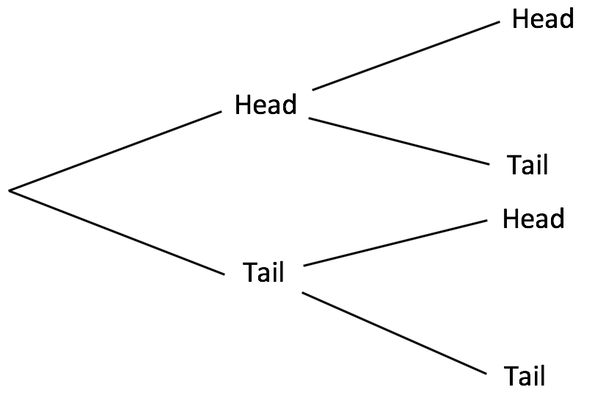
1) I flip a coin two times.
a) Fill in the probability tree
1) I flip a coin two times.
a) Fill in the probability tree
Find the probability that:
b) The coin lands on a head both times
c) The coin lands on a head the first time and then a tail the second time
d) The coin lands on a tail both times
e) The coin lands on a head and a tail in any order
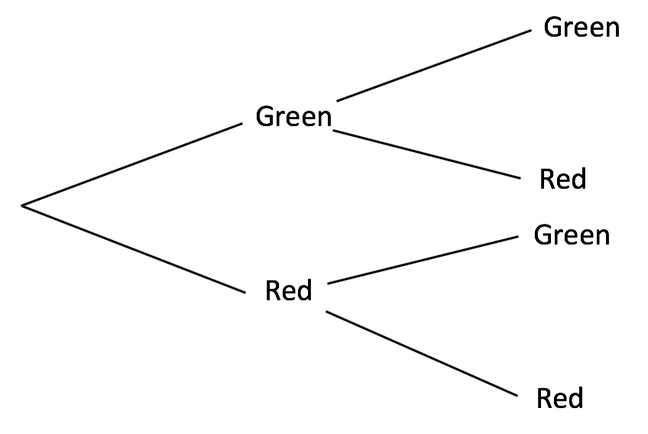
2) I have a bag that contains 3 green balls and 2 red balls. I pick a ball out of the bag, note the colour and then replace the ball. I pick a ball out of the bag twice.
a) Fill in the probability tree
b) The coin lands on a head both times
c) The coin lands on a head the first time and then a tail the second time
d) The coin lands on a tail both times
e) The coin lands on a head and a tail in any order
2) I have a bag that contains 3 green balls and 2 red balls. I pick a ball out of the bag, note the colour and then replace the ball. I pick a ball out of the bag twice.
a) Fill in the probability tree
Find the probability that:
b) Both of the balls are red
c) Both of the balls are green
d) I pick a red ball, and then a green ball
e) I pick a red and green ball in any order
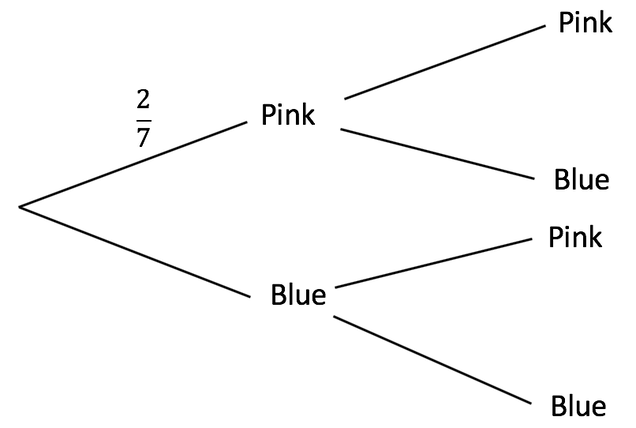
3) A bag contains balls that are either pink or blue. A ball is picked from the bag and then replaced. I pick a ball out of the bag twice.
a) Complete the probability tree diagram below.
b) Both of the balls are red
c) Both of the balls are green
d) I pick a red ball, and then a green ball
e) I pick a red and green ball in any order
3) A bag contains balls that are either pink or blue. A ball is picked from the bag and then replaced. I pick a ball out of the bag twice.
a) Complete the probability tree diagram below.
Find the probability of the following events occurring:
b) Two blue balls are picked
c) A pink ball is picked first and then a blue ball is picked second
d) Two pink balls are picked out of the bag
e) A blue and a pink ball are picked out in any order
f) Given that the first ball that is picked out is pink, find the probability that the second ball is blue
g) Given that the first ball that is picked out is blue, find the probability that the second ball is pink
h) Given that I pick out at least one pink ball (either first or second), find the probability that the other ball is also pink
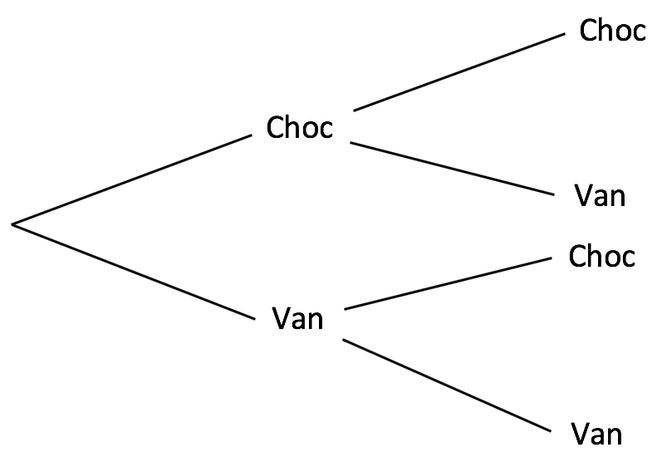
4) There are 6 chocolate cakes and 2 vanilla cakes in a tin. I take a cake at random from the tin and eat it (the cake is not replaced). I then take another cake at random from the tin and eat it.
a) Complete the probability tree diagram below.
b) Two blue balls are picked
c) A pink ball is picked first and then a blue ball is picked second
d) Two pink balls are picked out of the bag
e) A blue and a pink ball are picked out in any order
f) Given that the first ball that is picked out is pink, find the probability that the second ball is blue
g) Given that the first ball that is picked out is blue, find the probability that the second ball is pink
h) Given that I pick out at least one pink ball (either first or second), find the probability that the other ball is also pink
4) There are 6 chocolate cakes and 2 vanilla cakes in a tin. I take a cake at random from the tin and eat it (the cake is not replaced). I then take another cake at random from the tin and eat it.
a) Complete the probability tree diagram below.
Find the probabilities of the following events occurring:
b) Picking a chocolate and vanilla cake in either order
c) Picking two vanilla cakes
d) Picking two chocolate cakes
e) Picking a chocolate cake first and then a vanilla cake
f) Given that the first cake is chocolate, find the probability that the second cake is also chocolate
g) Given that the first cake is vanilla, find the probability that the second cake is chocolate
h) Given that the second cake is chocolate, find the probability that the first one was vanilla
i) Given that the second cake is vanilla, find the probability that the first cake is also vanilla
j) Given that one of the cakes is chocolate, find the probability that the other cake is also chocolate
k) Given that one of the cakes is vanilla, find the probability that the other cake is chocolate
b) Picking a chocolate and vanilla cake in either order
c) Picking two vanilla cakes
d) Picking two chocolate cakes
e) Picking a chocolate cake first and then a vanilla cake
f) Given that the first cake is chocolate, find the probability that the second cake is also chocolate
g) Given that the first cake is vanilla, find the probability that the second cake is chocolate
h) Given that the second cake is chocolate, find the probability that the first one was vanilla
i) Given that the second cake is vanilla, find the probability that the first cake is also vanilla
j) Given that one of the cakes is chocolate, find the probability that the other cake is also chocolate
k) Given that one of the cakes is vanilla, find the probability that the other cake is chocolate
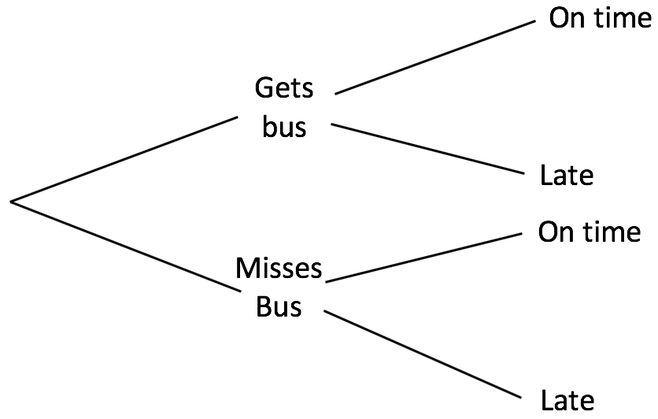
5) I get a bus to school. The probability that I miss the bus is 1/5. If I catch the bus, the probability that I am late for school is 0.1. If I miss the bus, the probability that I am late for school is 75%.
a) Complete the tree diagram below
Find the probability of the following events occurring:
b) Get the bus and am on time for school
c) Miss the bus and am late for school
d) Get the bus and am late for school
e) Miss the bus and am on time for school
f) Given that I am late for school, find the probability that I missed the bus
g) Given that I am late for school, find the probability that I got the bus
h) Given that I am on time for school, find the probability that I got the bus
i) Given that I am on time for school, find the probability that I missed the bus
b) Get the bus and am on time for school
c) Miss the bus and am late for school
d) Get the bus and am late for school
e) Miss the bus and am on time for school
f) Given that I am late for school, find the probability that I missed the bus
g) Given that I am late for school, find the probability that I got the bus
h) Given that I am on time for school, find the probability that I got the bus
i) Given that I am on time for school, find the probability that I missed the bus