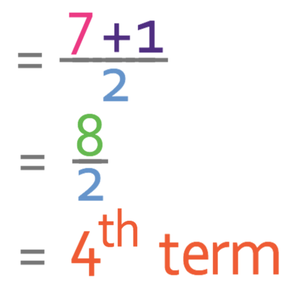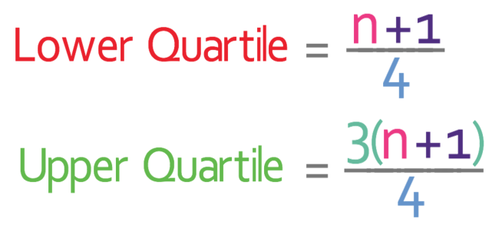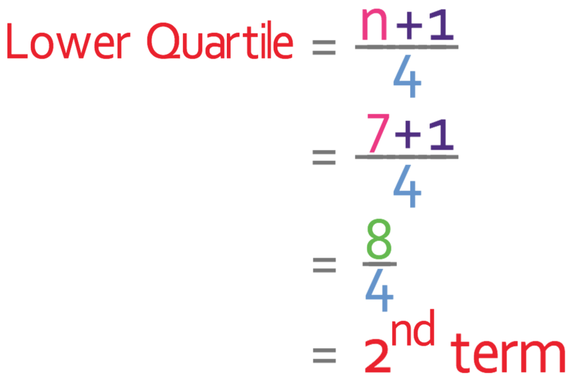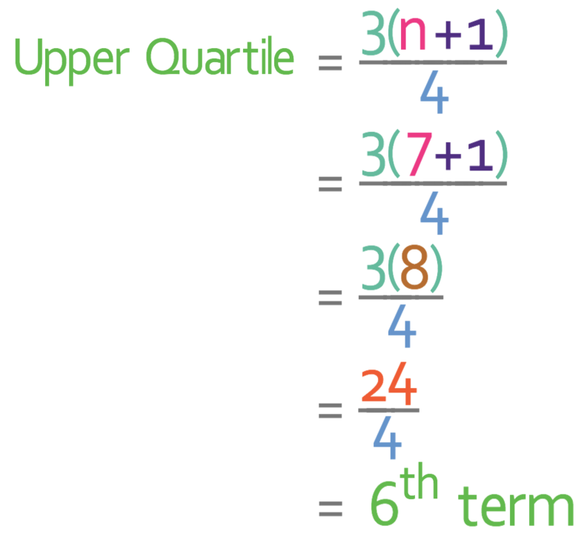6.3 G) Interquartile Range – Part 1
The range is not always particularly useful because it is affected by extreme values (either really small or really large values). For example, if we had the data for the incomes of individuals living in the UK, the range for the data set would be in the tens if not hundreds of millions. This is because the lowest income would be close to zero from individuals who are unemployed, and the highest income would be in the millions (likely be a football player, celebrity or a head of a company). These extremes would cause the range of our data to be very large.
This has led to statisticians creating what is known as the interquartile range, which measures the range of values in the middle 50% of the data. In other words, the interquartile range is the difference between the 25th percentile and the 75th percentile. It is worked out by using the following rule:
The upper quartile is the 75th percentile and is also known as Q3 or UQ. The lower quartile is the 25th percentile and is also known as Q1 or LQ (the median is known as Q2, but it is not relevant for the interquartile range).
We need to know the lower quartile, upper quartile and interquartile range when we are dealing with box plots.
Example 1
The incomes of 7 individuals are given below to the nearest £1000. What is the range and the interquartile range?
Range
The first part of the question asks us to work out what the range is for the data. The range is obtained by taking the lowest value from the highest value and the formula is shown below:
The highest income is £120,000 and the lowest income is £15,000. We sub these values into the formula.
The range of the incomes is £105,000 and this is very large. This is because the highest income of £120,000 is very large and it is increasing the range. Therefore, a better measure of the spread of data would be to use the interquartile range.
Median
Working out the interquartile range requires us to find the upper and lower quartiles. Obtaining the lower and upper quartiles is very similar to obtaining the median, so let’s find the median first to remind ourselves about how the median is obtained. In order to work out the median, we need to order the data from smallest to largest.
We use the formula below to find the position of the median term in the ordered data.
n in the above formula is the number of values/ observations in the data set. There are 7 values in the data set. Therefore, we sub in n as 7.
Therefore, the 4th term in the data is the median.
The median is £28,000.
We do not need to find the median to work out the interquartile range for the data, but the method for finding the median is very similar to the method for finding the lower and upper quartile.
Lower Quartile, Upper Quartile & Interquartile Range
The lower quartile is the 25th percentile, which can also be viewed as the median of the lower half of the data (it can be denoted as Q1 or LQ). The upper quartile is the 75th percentile, which can also be viewed as the median of the upper half of the data (it can be denoted as Q3 or UQ).
We can find what term the lower and upper quartile are in the ordered data by using the following formulas:
n in the above formulas is the number of values/ observations. The above formulas will always be the formulas for working out the lower and upper quartile, so it is worth getting the formulas down on a revision card.
Let’s work out the lower quartile first. The first step in finding the lower quartile is to find which term in the ordered data is the lower quartile. We do this by using the lower quartile formula (which is shown above). n in the formula is the number of values/ observations. There are 7 incomes, so we sub n as 7 into the lower quartile term formula.
This tells us that the lower quartile is the 2nd term in the ordered data.
The second term is £23,000, which means that the lower quartile is £23,000.
Now let’s find the upper quartile. The first step in finding the upper quartile is to find the term in the ordered data that is the upper quartile. We are able to do this by using the upper quartile term formula and subbing in n as 7.
The upper quartile is the 6th term in the ordered data.
The upper quartile is £45,000.
The final step is to use these values to find the interquartile range. The formula for the interquartile range is given below:
The upper quartile is £45,000 and the lower quartile is £23,000; we can sub these values into the formula.
The interquartile range for the date above is £22,000.
An extension for this question is to draw a boxplot. There is a separate section that is dedicated to drawing box plots. Click here to be taken through to the section about box plots.
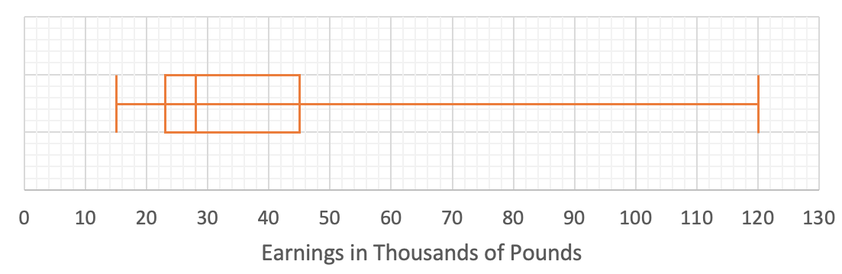
A box plot is a visual representation of the data. A box plot shows 5 values, which are:
- Lowest value
- Lower quartile
- Median
- Upper quartile
- Highest value
We have all of this information from the example above. The box plot for the above data looks like what is given below: