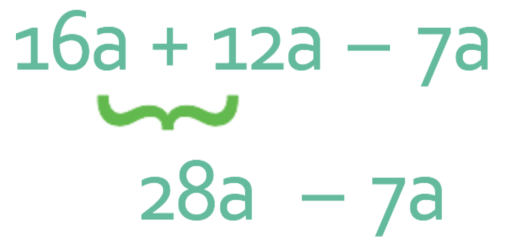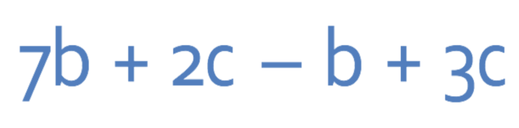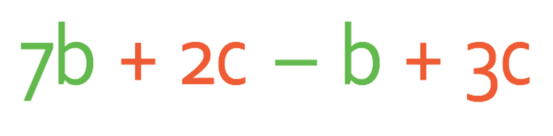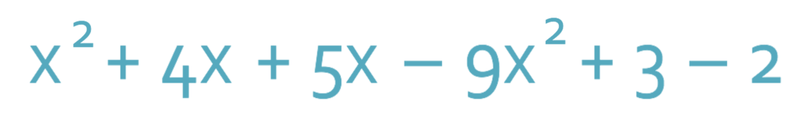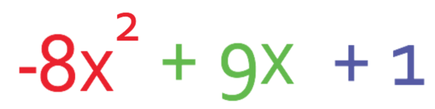Back to OCR Algebra Introduction (F) Home
2.1 B) Simplifying Expressions – Part 1
2.1 B) Simplifying Expressions – Part 1
Whenever we have an algebraic expression, we should always give our answer in it’s simplest form.
There are two different types of simplifying. These are collecting like terms and using letters and numbers. Collecting like terms is used when we are adding or subtracting terms. Letters and numbers are used when we are multiplying or dividing expressions.
In this section, we are going to be simplifying by collecting like terms and in the next section, we are going to be simplifying by using letters and numbers.
There are two different types of simplifying. These are collecting like terms and using letters and numbers. Collecting like terms is used when we are adding or subtracting terms. Letters and numbers are used when we are multiplying or dividing expressions.
In this section, we are going to be simplifying by collecting like terms and in the next section, we are going to be simplifying by using letters and numbers.
Collecting Like Terms
One way to think about collecting like terms is to imagine that someone asks you how many video games you have. If someone asked you this, you would give the total number of games that you have. For example, I have 12 video games. You would not say, “I have 7 video games and I also have 5 video games”; you would just give the total number of video games that you have.
To collect like terms, we bring terms that are of the same type together. When we are bringing like terms together, we need to remember to include the signs before the terms that we are combining.
One way to think about collecting like terms is to imagine that someone asks you how many video games you have. If someone asked you this, you would give the total number of games that you have. For example, I have 12 video games. You would not say, “I have 7 video games and I also have 5 video games”; you would just give the total number of video games that you have.
To collect like terms, we bring terms that are of the same type together. When we are bringing like terms together, we need to remember to include the signs before the terms that we are combining.
Example 1
Simplify the expression below.
Simplify the expression below.
All of the terms above are a, which means that we can collect all of them together.
Let’s start by combing the first two terms together; 16a + 12a, which is 28a.
Let’s start by combing the first two terms together; 16a + 12a, which is 28a.
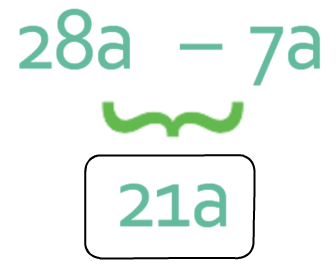
We can now collect these two terms together.
This expression simplifies to give 21a.
Example 2
Simplify the expression below.
Simplify the expression below.
There are two different unknowns in this expression; b and c. To simplify this expression, we collect the terms that only have a b in them and then collect the terms that only have a c in them. You may find that it is useful to highlight the different types of terms in a different colour. When we are highlighting the terms, we need to remember to highlight both the term and the sign that is in front of the term. I have changed all of the terms that only have b in them to green and all of the terms that only have c in them to orange.
The “– b” in the expression means – 1b; whenever we have an unknown by itself, it means 1 lot of that unknown (for example, if I said that I had an apple for lunch, it would mean that I had one apple for lunch. If I ate more than one apple for lunch, I would have said that I had eaten 2 apples). Feel free to place a 1 in front of the b if you find it easier.
Therefore, we combine the b’s (7b – b) to get 6b. And, we combine the c’s (2c + 3c) to get 5c.
Therefore, we combine the b’s (7b – b) to get 6b. And, we combine the c’s (2c + 3c) to get 5c.
Example 3
Simplify the expression below.
Simplify the expression below.
There are 3 different types of terms in this equation; x2, x and numbers; x2 and x need to be treated as different types of terms although they both contain the same letter.
To help me combine the three different types of terms, I have made all of the x2 terms red, x terms green and number blue. When changing the colour of the terms, I have made sure that I also change the colour of the sign before the term.
We now collect the x2 terms (x2 – 9x2) to get -8x2, the x’s (4x + 5x) to get 9x, and the numbers (3 – 2) to get 1. The simplified expression becomes.