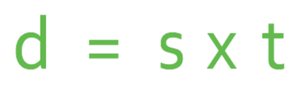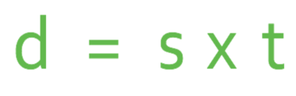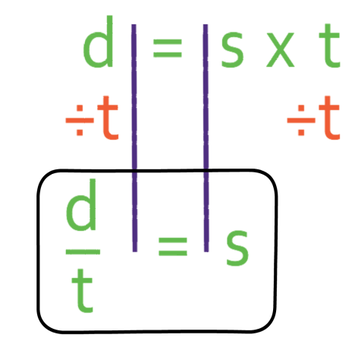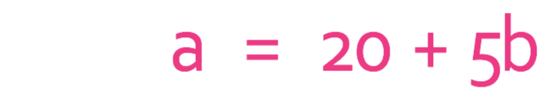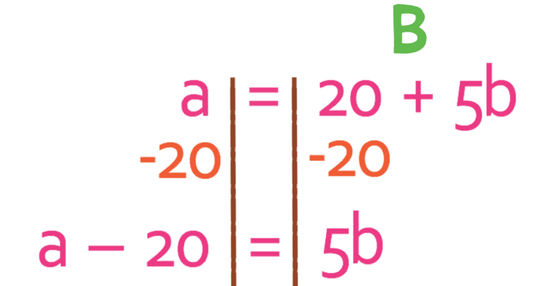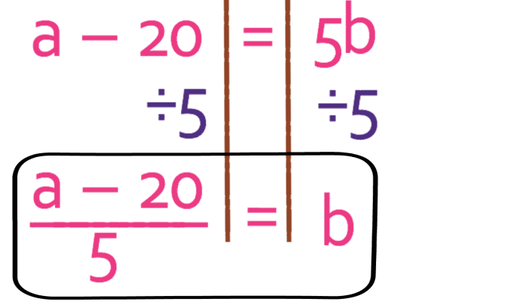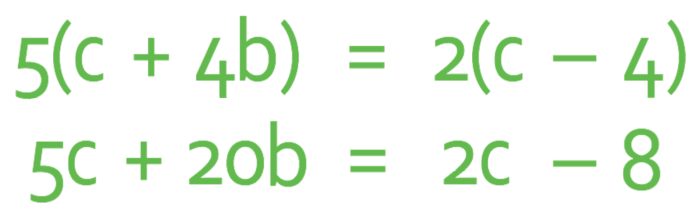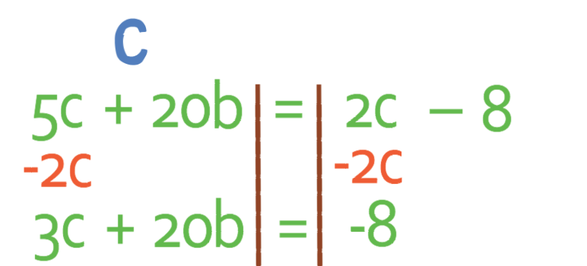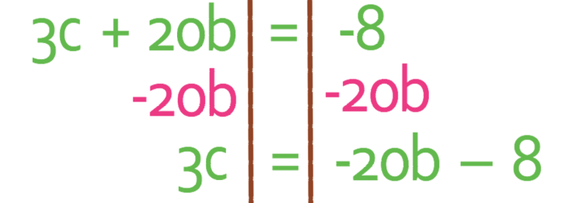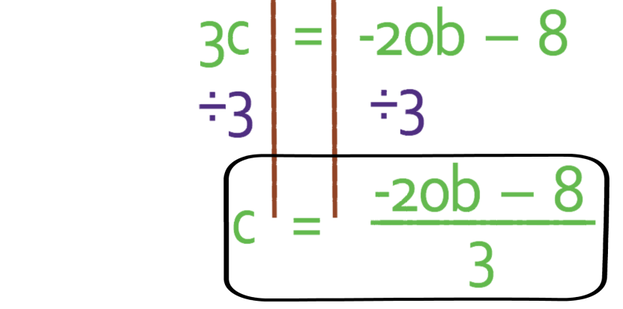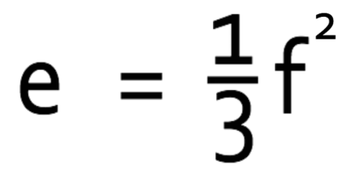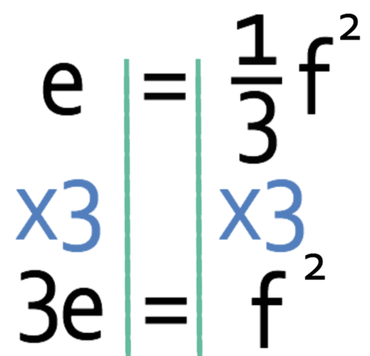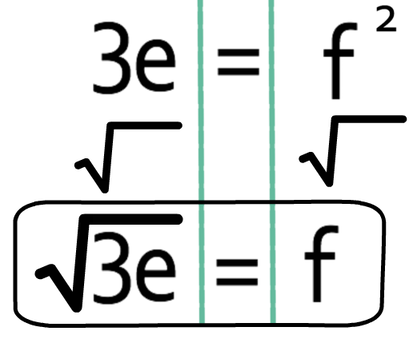Back to OCR Algebraic Formulae (F) Home
2.3 C) Rearranging Formulas – Part 1
2.3 C) Rearranging Formulas – Part 1
In the questions that we have looked at so far in this whole section, we have been given formulas that have the variable that we are looking for equal to a calculation involving all of the other variables; the variable that we were looking for was the subject of the formula.
For example, in the first example that we looked at in this whole section, we used the formula below to find out the value of d.
For example, in the first example that we looked at in this whole section, we used the formula below to find out the value of d.
This was straightforward because d was the subject of the formula, which meant that we sub the other values that we were given into the equation and this gave us the value for d.
However, if we were asked to find the value of s or t, the formula above is not as useful as it could be. It is for this reason that we may want to rearrange a formula so that the subject of the formula is the unknown variable that we are finding.
Currently, the subject of the equation above is d. Let’s now make s the subject of the formula.
However, if we were asked to find the value of s or t, the formula above is not as useful as it could be. It is for this reason that we may want to rearrange a formula so that the subject of the formula is the unknown variable that we are finding.
Currently, the subject of the equation above is d. Let’s now make s the subject of the formula.
Currently, s in the formula is being multiplied by t. In order to make s the subject of the formula, we need to do the opposite of multiplying by t, which is dividing by t. Therefore, we divide both sides of the formula by t.
We now have s as the subject of the formula, which makes the formula easier to find the value of s when we are given the value of d and t.
You may think that this is a little bit pointless to rearrange the formula above, which it kind of is, but rearranging a formula to make the variable that you are finding out the subject is very useful when we have more complex formulas. Throughout this section and the next few sections, you will see how to rearrange more complex formulas.
You may think that this is a little bit pointless to rearrange the formula above, which it kind of is, but rearranging a formula to make the variable that you are finding out the subject is very useful when we have more complex formulas. Throughout this section and the next few sections, you will see how to rearrange more complex formulas.
Simple Examples
Example 1
Make b the subject of the formula below.
Example 1
Make b the subject of the formula below.
The first step is to get the unknown that we want to be the subject to one side of the formula and everything else to the other side. We want to have b the subject and currently there is 20 + 5b on the right-hand side of the formula. Therefore, we need to move the 20 from the right to the left side of the formula, which we are able to do by taking 20 from both sides of the formula (the opposite of positive 20).
The next step is to divide both sides of the formula by 5. This is because we want to have b the subject and not 5b.
Example 2
Make c the subject of the formula below.
Make c the subject of the formula below.
The first step to answering this question is to expand both of the brackets out. We expand the brackets by multiplying the number that is on the outside of the brackets by all of the terms that are on the inside of the brackets. This gives us.
The next step is to get all of the terms that contain the unknown that we are making the subject to one side of the formula, and all of the other terms to the other side. We are making c the subject. It is easier to move all of the c’s to the side that currently has the most c’s, which is the left side of the formula. This means that we will be moving the 2c from the right side of the formula to the left and we do this by taking 2c from both sides.
We want to have the unknown that we are making the subject of the formula on its own. This means that we need to move the 20b from the left side of the formula to the right side of the formula, which we do by taking 20b from both sides of the formula.
We want c to be the subject of the formula and not 3c. This means that we need to divide both sides of the equation by 3.
Example 3
Make f the subject of the formula below.
Make f the subject of the formula below.
This formula has all of the terms that contain f on the right side of the formula and all of the other terms on the left side. On the right side of the formula, we have one third of the square of f and we want to make just f the subject of the formula. There are a few different methods that can be used to make f the subject, but I think that the best method is to go about making the square of f the subject, and then square root.
Currently, we have one third of the f squared or the f squared divided by 3. To get rid of the fraction, we multiply both sides of the formula by the denominator of the fraction. The denominator of the fraction is 3, so we multiply both sides of the formula by 3.
Currently, we have one third of the f squared or the f squared divided by 3. To get rid of the fraction, we multiply both sides of the formula by the denominator of the fraction. The denominator of the fraction is 3, so we multiply both sides of the formula by 3.
We are making f the subject and not the square of f. We can obtain f by square rooting both sides of the formula. This gives us:
We now have f as the subject of the formula.