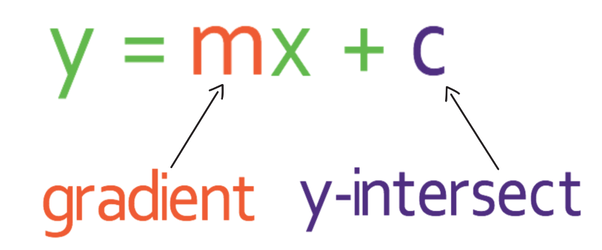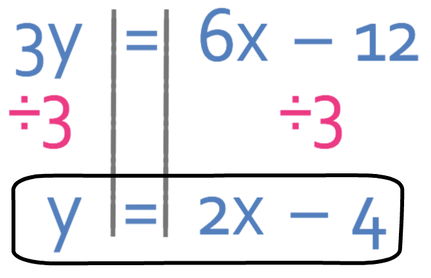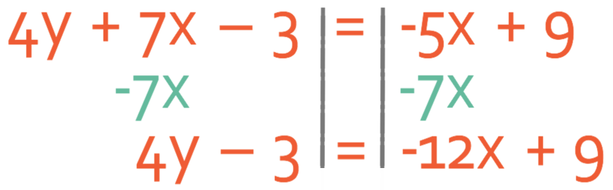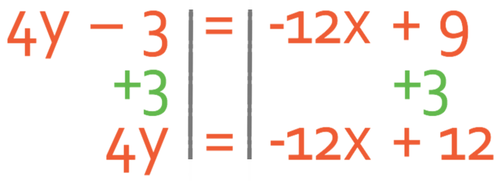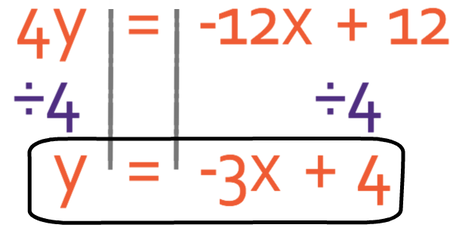Back to OCR Linear Graphs (F) Home
2.5 C) General Linear Graph Form
2.5 C) General Linear Graph Form
In the previous section we learnt that there are two types of linear graphs;
In this section we are going to be looking at upwards or downwards sloping graphs. Upwards and downwards sloping graphs take the form y = mx + c, where m is the gradient and c is the y intercept (we will be looking at the gradient and y intercept in more detail later).
- Vertical and horizontal graphs
- Upwards or downwards sloping graphs
In this section we are going to be looking at upwards or downwards sloping graphs. Upwards and downwards sloping graphs take the form y = mx + c, where m is the gradient and c is the y intercept (we will be looking at the gradient and y intercept in more detail later).
If an equation is not already in this form, we are able to rearrange an equation into the form of y = mx + c; we are essentially making y the subject.
It is so much easier to have a graph in the form y = mx + c because when it is in this form, we are easily able to see the gradient of the line (the value of m) and the y intercept (the value of c).
Let’s have a few graphs that we are going to rearrange to get them in the form y = mx + c.
It is so much easier to have a graph in the form y = mx + c because when it is in this form, we are easily able to see the gradient of the line (the value of m) and the y intercept (the value of c).
Let’s have a few graphs that we are going to rearrange to get them in the form y = mx + c.
Example 1
We have the equation 3y = 6x – 12. Rearrange the equation into the form y = mx + c and find the gradient and the y intercept.
We have the equation 3y = 6x – 12. Rearrange the equation into the form y = mx + c and find the gradient and the y intercept.
Currently this equation is saying that 3y is equal to something. However, we do not want 3y and instead want to have y equal to something. Therefore, we need to divide both sides of the equation by 3.
We now have the graph in the form of y = mx + c. Therefore, we can say that the gradient of the line is 2 (the value for m) and the y intercept is -4 (the value of c).
Example 2
We have the equation 4y + 7x – 3 = -5x + 9. Rearrange the equation into the form y = mx + c and find the gradient and the y intercept.
We have the equation 4y + 7x – 3 = -5x + 9. Rearrange the equation into the form y = mx + c and find the gradient and the y intercept.
To get the equation into the form y = mx + c, we are essentially making y the subject of the equation. We do this by getting all of the y terms to one side of the equation and all of the other terms to the other side of the equation. We get the y terms to the side of the equation that currently has more y’s. Currently, there are 4 y’s on the left and no y’s on the right. Therefore, we should keep the y’s on the left side of the equation (because 4y is greater than 0y) and have all of the other terms on the right side of the equation. This means that we need to move 7x and -3 from the right side of the equation to the left.
Let’s start by moving the 7x across. We are able to move it across by doing the opposite, and the opposite of adding 7x is taking 7x. Therefore, we take 7x from both sides of the equation.
Let’s start by moving the 7x across. We are able to move it across by doing the opposite, and the opposite of adding 7x is taking 7x. Therefore, we take 7x from both sides of the equation.
I am now going to move the -3 from the left side of the equation to the right. We are able to move the -3 by doing the opposite, and the opposite of taking 3 is adding 3. Therefore, we add 3 to both sides of the equation.
We want to have y is equal to something and not 4y is equal to something. Therefore, we need to divide both sides of the equation by 4.
The equation is now in the form y = mx + c. Therefore, we can see that the gradient is -3 and the y intercept is 3.