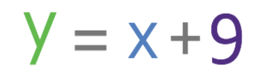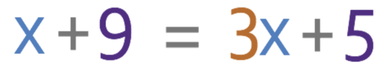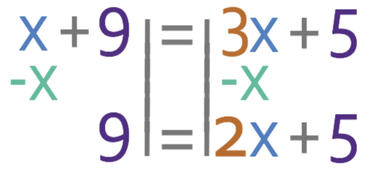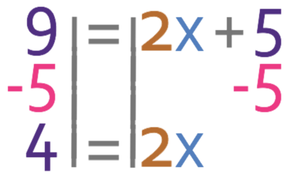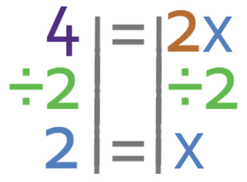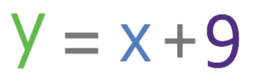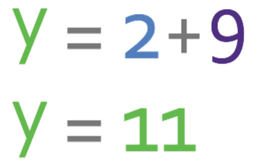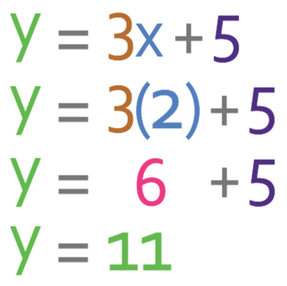Back to OCR Linear Graphs (F) Home
2.5 K) Finding the Point of Intersection Between Two Lines
2.5 K) Finding the Point of Intersection Between Two Lines
The general form of a linear line is y = mx + c. m in this formula is the gradient and c is the y intercept. The gradient refers to the slope of a line. The gradient is a measure of how much y changes when x increases by 1.
It may be the case in the exam that you will need to find the coordinates of the point where two lines intersect one another. For example, we have two lines; line A and line B. Line A has the equation y = x + 9 and line B has the equation y = 3x + 5. Find the coordinates for the point of intersection between the two lines.
It may be the case in the exam that you will need to find the coordinates of the point where two lines intersect one another. For example, we have two lines; line A and line B. Line A has the equation y = x + 9 and line B has the equation y = 3x + 5. Find the coordinates for the point of intersection between the two lines.
Questions like this are essential simultaneous equation questions and we have looked at simultaneous equations in a different section (click here to be taken through to the simultaneous equations section). However, the method that we can use to answer these types of questions can be slightly different to the usual methods used to answer simultaneous equations because both of the equations are given in the form of y = “something”. For the above example, line A tells us that y is equal to x + 9 and line B tells us that y is equal to 3x + 5. For the point of intersection between the two lines, y must be the same for both of the equations/ lines. This means that x + 9 must equal 3x + 5. This gives us the equation below.
We now have an equation that only has one unknown, which means that we are able to find out what x is. We are able to find the value of x by getting all of the x’s on one side of the equation and all of the numbers on the other side of the equation. We get the x’s to the side of the equation where there are currently more x’s. Currently there are more x’s on the right because 3x is more than x (1x). Therefore, we need to get all of the x’s to the right and all of the numbers to the left. This means that we need to move the x that is on the left side of the equation to the right and we are able to do this by taking x from both sides of the equation.
The next step is to move the + 5 from the right side of the equation to the left. We are able to do this by doing the opposite and the opposite of adding 5 is taking 5, so we take 5 from both sides of the equation.
We want to find the value of x and not 2x. Therefore, we need to divide both sides of the equation by 2.
This tells us that x is 2 and this is the x coordinate for the point of intersection between line A and line B.
We now need to find the y coordinate for the point of intersection. We do this by subbing the x coordinate that we have just found into the equation of one of the lines. It does not matter which line we use; I am going to use line A, which has the equation:
We now need to find the y coordinate for the point of intersection. We do this by subbing the x coordinate that we have just found into the equation of one of the lines. It does not matter which line we use; I am going to use line A, which has the equation:
We found that the x coordinate was 2, so we sub in x as 2 into the equation.
This tells us that the y coordinate of the point of intersection between line A and line B is 11. Therefore, the coordinates for the point of intersection between line A and line B are (2, 11). We can check that we have the correct coordinates for the point of intersection by subbing the values for x (2) and y (11) that we have just obtained into the other line equation; we used line A, so we would check our point of intersection by subbing x and y into line B (if we used line B to find the y coordinate, we would use line A to check). If the equation works when we sub our values for x and y in, we have obtained the correct answer. If the equation does not work when we sub our values for x and y in, it means that we have not found the correct coordinates of intersection.
I am going to check by subbing x in as 2 and y in as 11 into the equation for line B. The working is shown below.
I am going to check by subbing x in as 2 and y in as 11 into the equation for line B. The working is shown below.
The equation works, which means that we have found the correct coordinates for the point of intersection between line A and line B; the coordinates for the point of intersection are (2, 11).
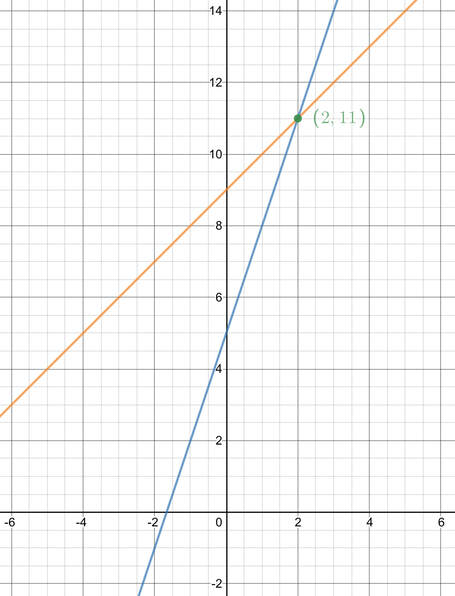
I have plotted the two lines on the graph below; line A is in blue and line B is in orange. From the graph, you can see that the point of intersection is (2, 11).
I have plotted the two lines on the graph below; line A is in blue and line B is in orange. From the graph, you can see that the point of intersection is (2, 11).
End Note
Whenever we are answering questions like this, we need to be very careful that both of the equations for the lines are in the form of y = “something”. This is because if they are not in this form, we cannot say that at the point of intersection, one equation is equal to the other equation.
For example, let’s suppose that we are looking for the point of intersection between the two lines below:
Whenever we are answering questions like this, we need to be very careful that both of the equations for the lines are in the form of y = “something”. This is because if they are not in this form, we cannot say that at the point of intersection, one equation is equal to the other equation.
For example, let’s suppose that we are looking for the point of intersection between the two lines below:
- Line A: y = 3x – 7
- Line B: 2y = -10x + 4