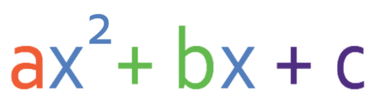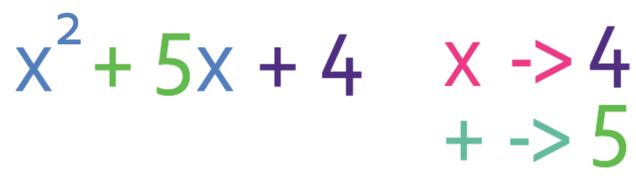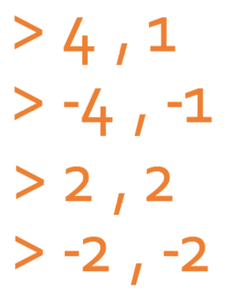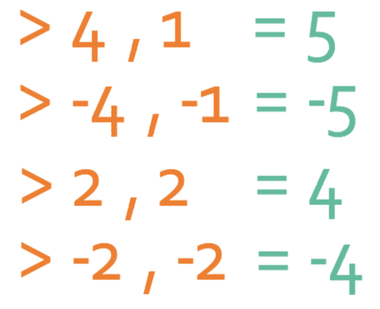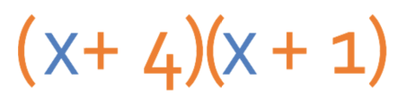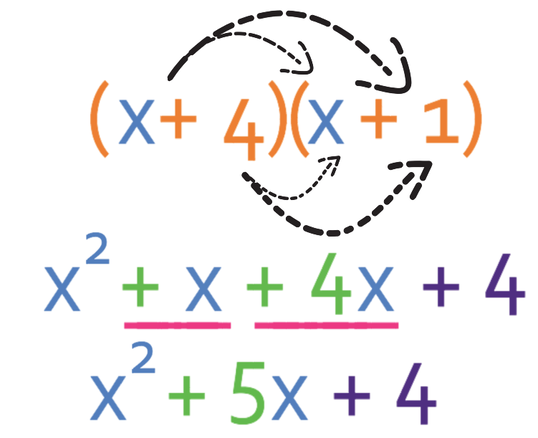Back to OCR Quadratic Equations: Factorising (F) Home
2.6 A) Factorising Quadratics (A = 1) – Part 1
2.6 A) Factorising Quadratics (A = 1) – Part 1
Quadratics equations are equations that have the highest power of an unknown as 2 (squared). They take the form:
The values for a, b and c can be positive or negative.
For example, suppose that we had the quadratic equation:
For example, suppose that we had the quadratic equation:
The value for a is 1, b is 5 and c is 4.
In this section, we are going to be looking at factorising quadratic equations that have a value for a as 1 (like the first quadratic equation that we looked at). We will be factorising equations that have a value for a that is greater than 1 later on in this section.
When we are factorising quadratic equations with a value for a as 1, we are going to get what is shown below:
In this section, we are going to be looking at factorising quadratic equations that have a value for a as 1 (like the first quadratic equation that we looked at). We will be factorising equations that have a value for a that is greater than 1 later on in this section.
When we are factorising quadratic equations with a value for a as 1, we are going to get what is shown below:
The question marks can be positive or negative numbers. The values of the question marks are found by finding two numbers that multiply together to give the value of c, and add together to give the value of b.
Example 1
Factorise the quadratic:
Factorise the quadratic:
This quadratic has a value of a as 1, which means that the factorised form will be (x + ?)(x + ?). We find the values of the question marks in the brackets by finding two numbers that multiply together to give c (4), and add together to give us the value of b (5). The easiest way to find the values of the question marks is to write down all of the pairs of numbers that multiply together to give us 4 (the value of (c)). 4 is positive, which means that either both of the numbers in the pairs will be positive, or both of the numbers will be negative. After we have these pairs of values, we can see which pair adds together to give 5.
The pairs of values that multiply together to give 4 are:
The next step is to find the pair of numbers that add together to give 5. The pairs above add together to give the following:
We can see that the only pair that adds together to give 5 is the first pair. Therefore, the factorised answer for this question is:
The order that we place the numbers into the brackets does not matter; the answer could have been written as (x + 1)(x + 4).
We are able to check that we have factorised correctly by expanding the brackets and seeing if we get the expression that we were factorising. I am going to expand the bracket using the FOIL technique (First, Outer, Inner, Last).
We are able to check that we have factorised correctly by expanding the brackets and seeing if we get the expression that we were factorising. I am going to expand the bracket using the FOIL technique (First, Outer, Inner, Last).
The expanded brackets gives us the same expression that we were factorising, which means that we have factorised correctly.