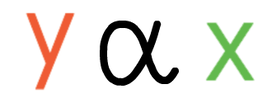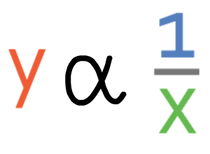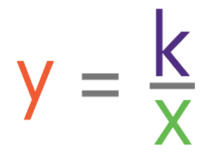Back to OCR Direct & Inverse Proportion (F) Home
3.1 F) Direct & Inverse Proportion Graphs
3.1 F) Direct & Inverse Proportion Graphs
From the previous sections, we have learnt about direct and inverse proportion. In this section we are going to be looking at drawing the graphs for direct and inverse proportion.
Direct Proportion
Direct proportion is where the variables move in the same direction and by the same proportion. As one variable increases, so too does the other variable. And, when one variable decreases, so too does the other variable. The notation and the general equation for y being directly proportional to x are shown below:
Direct proportion is where the variables move in the same direction and by the same proportion. As one variable increases, so too does the other variable. And, when one variable decreases, so too does the other variable. The notation and the general equation for y being directly proportional to x are shown below:
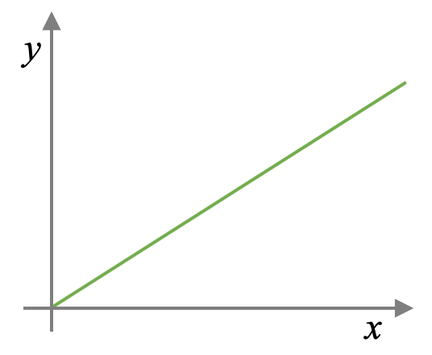
The graph for direct proportion is shown below.
All direct proportion graphs start from where both of the variables are 0. This is the case even if a square, cube or root is involved.
The general form for direct proportion is very similar to the equation of a linear line. The steepness of the line depends on the value of k; a greater value of k will result in the line being steeper and a smaller value of k will result in the line being flatter. You can think of k as the gradient of the line.
The general form for direct proportion is very similar to the equation of a linear line. The steepness of the line depends on the value of k; a greater value of k will result in the line being steeper and a smaller value of k will result in the line being flatter. You can think of k as the gradient of the line.
Inverse Proportion
Inverse proportion is where the variables move in opposite directions. As one variable increases, the other decreases. And, when one variable decreases, the other increases. The notation and general equation for y being inversely proportional to x are shown below:
Inverse proportion is where the variables move in opposite directions. As one variable increases, the other decreases. And, when one variable decreases, the other increases. The notation and general equation for y being inversely proportional to x are shown below:
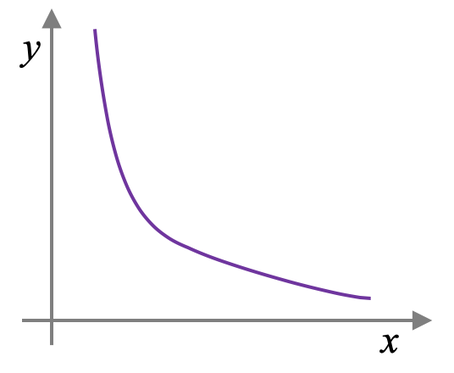
The graph for inverse proportion is shown below.
The general equation for inverse proportion looks very similar to a reciprocal graph; reciprocal graphs take the form y = 1/x. The difference between a reciprocal graph and the equation for inverse proportion is that inverse proportion has k/x and a reciprocal graph has 1/x. Therefore, whenever you are drawing/ spotting an inverse proportion graph, imagine that you are drawing/ spotting a reciprocal graph.
Final Point
The graphs for direct and inverse proportion are very easy to forget. Therefore, it is worth getting them down on a revision card so that you do not forget them.
The graphs for direct and inverse proportion are very easy to forget. Therefore, it is worth getting them down on a revision card so that you do not forget them.