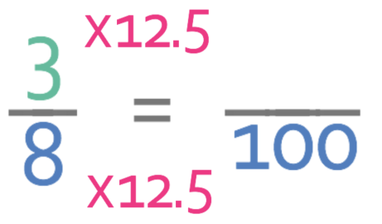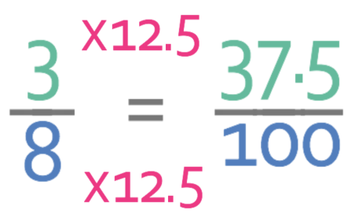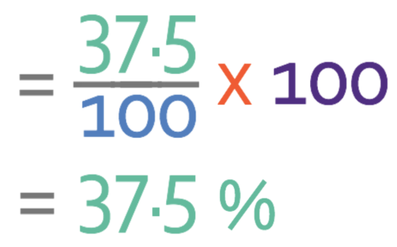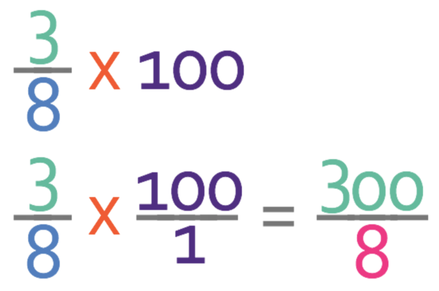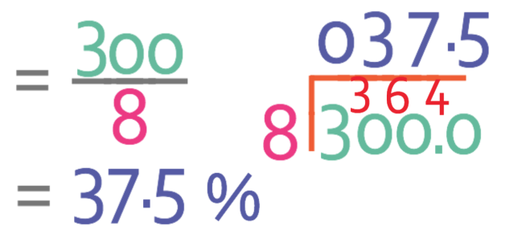Back to OCR Percentages (F) Home
3.2 D) Converting Fractions into Percentages - Part 2
3.2 D) Converting Fractions into Percentages - Part 2
The content in this section builds on the content that was looked at in the previous section. Make sure that you have worked through part 1 first (click here to be taken through to part 1).
Example 3
What is the fraction below as a percentage? Do not use a calculator.
What is the fraction below as a percentage? Do not use a calculator.
Method 1 – Denominator Becoming 100
Currently the denominator of our fraction is 8 and we want our denominator to be 100. We can find out what we need to multiply our denominator by to get 100, by dividing our desired denominator (100) by the current denominator (8). I am going to use the bus stop method to see what 100 ÷ 8 is.
Currently the denominator of our fraction is 8 and we want our denominator to be 100. We can find out what we need to multiply our denominator by to get 100, by dividing our desired denominator (100) by the current denominator (8). I am going to use the bus stop method to see what 100 ÷ 8 is.
100 divided by 8 is 12.5. This method is all about creating equivalent fractions with 100 being the denominator of the new fraction. This means that we need to multiply both the numerator and the denominator of our fraction by 12.5.
The easiest way to multiply 3 by 12.5 is to split 12.5 into the 3 different components that it is made from and multiply each of these value by 3; we can split 12.5 into 10, 2 and 0.5. We then add the values that we obtain.
The numerator of the fraction will be 37.5 and the denominator will be 100.
- 10 x 3 = 30
- 2 x 3 = 6
- 0.5 x 3 = 1.5
- 30 + 6 + 1.5 = 37.5
The numerator of the fraction will be 37.5 and the denominator will be 100.
The final step in this method is to multiply our equivalent fraction by 100.
Multiplying a fraction by the value of the denominator eliminates the denominator, which just leaves the numerator of our fraction. Therefore, our fraction as a percentage is 37.5%.
Note: usually we will never have a fraction with a numerator that is a decimal, but it is fine to have a numerator as a decimal when we are converting fractions into percentages.
Note: usually we will never have a fraction with a numerator that is a decimal, but it is fine to have a numerator as a decimal when we are converting fractions into percentages.
Method 2 – Multiplying the Fraction by 100
In this method we just multiply the fraction by 100. I am going to place the 100 (the integer) over 1 to make it easier to multiply across.
In this method we just multiply the fraction by 100. I am going to place the 100 (the integer) over 1 to make it easier to multiply across.
The next step is to convert this fraction into a decimal. We convert the fraction into a decimal by dividing the numerator by the denominator. I am going to use the bus stop method to work this out.
This gives us 37.5, which means that our percentage is 37.5%.
Summary
It does not matter which method you use when converting fractions to percentages; you just need to be comfortable using your chosen method. There are quite a few questions in the quiz and I have gone through the answers using both of the methods. Try using both methods for a few questions in the quiz and see which method you prefer.
It does not matter which method you use when converting fractions to percentages; you just need to be comfortable using your chosen method. There are quite a few questions in the quiz and I have gone through the answers using both of the methods. Try using both methods for a few questions in the quiz and see which method you prefer.