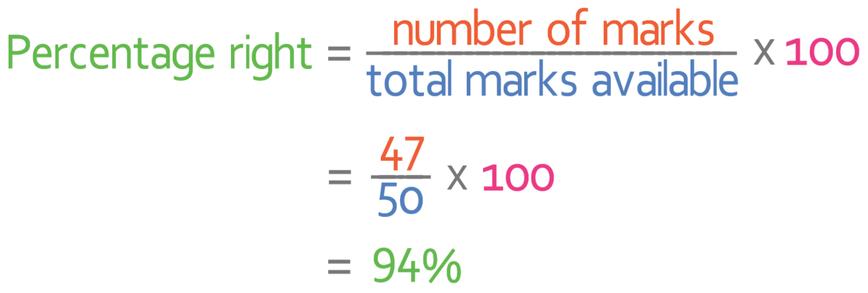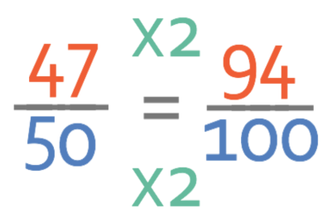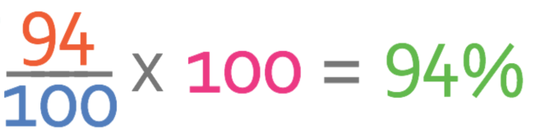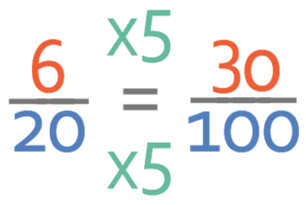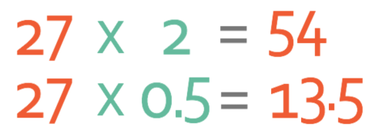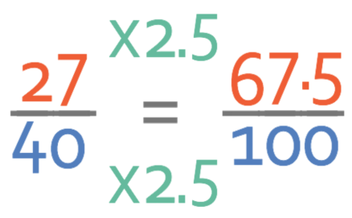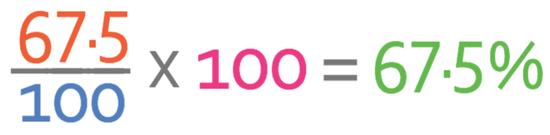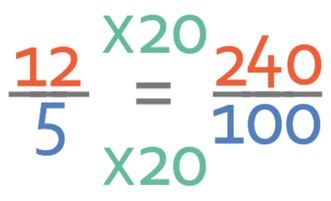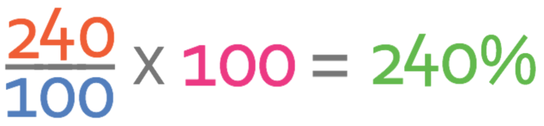Back to OCR Percentages (F) Home
3.2 J) Expressing One Number as a Percentage of Another
3.2 J) Expressing One Number as a Percentage of Another
The most obvious example of where we do this is when we work out the percentage that someone scored on a test and we use the percentages to determine what grade an individual gets or whether they pass or fail the test.
Example 1
For example, on the driving theory test, there is a multiple-choice section where you need to get 86% of the answers right to pass. If you get less than 86% right, you fail the test and then have to retake the test before you are able to take your practical test and then be able to drive by yourself (however, there is a second component of the theory test, which is known as hazard perception. You have to pass both the hazard perception and multiple-choice sections to pass the theory test).
We are able to express one number as a percentage of another by dividing the first number by the second number and multiplying by 100. For example, the multiple-choice part of the theory test is out of 50 marks. An individual sits the test and scores 47 marks. What percentage of marks did they get correct and did they pass the multiple-choice section of the theory test?
We are told that the individual scored 47 marks and the test was out of 50. We can find the percentage that this individual got correct by dividing the marks that they obtained (47) by the total marks that were available for the test (50). The final step is then to multiply by 100.
For example, on the driving theory test, there is a multiple-choice section where you need to get 86% of the answers right to pass. If you get less than 86% right, you fail the test and then have to retake the test before you are able to take your practical test and then be able to drive by yourself (however, there is a second component of the theory test, which is known as hazard perception. You have to pass both the hazard perception and multiple-choice sections to pass the theory test).
We are able to express one number as a percentage of another by dividing the first number by the second number and multiplying by 100. For example, the multiple-choice part of the theory test is out of 50 marks. An individual sits the test and scores 47 marks. What percentage of marks did they get correct and did they pass the multiple-choice section of the theory test?
We are told that the individual scored 47 marks and the test was out of 50. We can find the percentage that this individual got correct by dividing the marks that they obtained (47) by the total marks that were available for the test (50). The final step is then to multiply by 100.
This individual got 94% of the marks right, which is above the percentage needed to pass the multiple-choice section of the theory test.
Non-Calculator
When we have access to a calculator, we just type what we have above into a calculator. When we do not have access to a calculator, it is best to get the denominator of the fraction over 100. This is so that when we multiply by 100, the divide by 100 (which comes from the denominator of the fraction) and the multiply by 100 cancel each other out. This leads to the numerator being the percentage.
Let’s do this for the above example.
Non-Calculator
When we have access to a calculator, we just type what we have above into a calculator. When we do not have access to a calculator, it is best to get the denominator of the fraction over 100. This is so that when we multiply by 100, the divide by 100 (which comes from the denominator of the fraction) and the multiply by 100 cancel each other out. This leads to the numerator being the percentage.
Let’s do this for the above example.
The whole aim of this method is to make the denominator equal to 100 (we do not care what the numerator of the fraction is at this stage). The denominator in the fraction above is 50. We can multiply it by 2 to make it equal 100 (to find out what number we need to multiply the denominator by to give 100, we divide 100 by the current denominator. The current denominator is 50, so when we divide 100 by 50, we get 2, which tells us that we need to multiply by 2). As we are creating an equivalent fraction, we need to multiply the numerator by 2 as well. The numerator of the fraction becomes 94.
We are able to convert this fraction into a percentage by multiplying by 100.
The divide by 100 (from the fraction) and multiply by 100 cancel each other out. This just leaves the numerator as the percentage. Therefore, the percentage that they got right on the test was 94%, and this is the same percentage that we got when we used the calculator.
Example 2
I am in a shop and am buying some cookies. I see a promotional pack of 20 cookies that has 6 cookies free (there are 26 cookies in the packet). What percentage of the original packet do I get for free? Do not use a calculator.
A normal pack contains 20 cookies and the promotional pack contains 26 cookies, which means that I get 6 free cookies. We can place this information into a fraction. The numerator will be the number of cookies that I get for free (6) and the denominator will be the number of the cookies that would come in a normal/ non-promotional packet (20). Therefore, my calculation is:
I am in a shop and am buying some cookies. I see a promotional pack of 20 cookies that has 6 cookies free (there are 26 cookies in the packet). What percentage of the original packet do I get for free? Do not use a calculator.
A normal pack contains 20 cookies and the promotional pack contains 26 cookies, which means that I get 6 free cookies. We can place this information into a fraction. The numerator will be the number of cookies that I get for free (6) and the denominator will be the number of the cookies that would come in a normal/ non-promotional packet (20). Therefore, my calculation is:
The next step is to get the denominator of the fraction to equal 100. To find of what we need to multiply the numerator and the denominator by to get the denominator to equal 100, we divide 100 by the current denominator. We therefore divide 100 by 20, which gives us 5. As we are finding equivalent fractions, we need to multiply the numerator and the denominator of the fraction by 5. The fraction becomes:
We are able to convert this fraction into a percentage by multiplying by 100.
The divide by 100 (from the fraction) and the multiply by 100 cancel one another out. This just leaves the numerator as the percentage. Therefore, I get 30% of the original pack for free.
Example 3
Example 3 is going to give us a numerator in our fraction that is not going to be an integer (our numerator will be a decimal). Usually we would NEVER have a numerator that is not an integer, but when we are working with percentages, it is fine to have a numerator that is not an integer. This is because the whole aim of the fraction method is to make the denominator of the fraction 100; we do not particularly care what the numerator of the fraction is. This will all make much more sense when we look through an example.
I am practicing my football shooting. I take 40 shots and get 27 shots on target. What percentage of the shots do I get on target? Do not use a calculator.
The numerator of the fraction is the number of shots that were on target and the denominator is going to be the number of shots that I took (out of 40 shots, 27 were on target). Therefore, the fraction is:
Example 3 is going to give us a numerator in our fraction that is not going to be an integer (our numerator will be a decimal). Usually we would NEVER have a numerator that is not an integer, but when we are working with percentages, it is fine to have a numerator that is not an integer. This is because the whole aim of the fraction method is to make the denominator of the fraction 100; we do not particularly care what the numerator of the fraction is. This will all make much more sense when we look through an example.
I am practicing my football shooting. I take 40 shots and get 27 shots on target. What percentage of the shots do I get on target? Do not use a calculator.
The numerator of the fraction is the number of shots that were on target and the denominator is going to be the number of shots that I took (out of 40 shots, 27 were on target). Therefore, the fraction is:
The next step is to get the denominator to equal 100. In order to find out what we need to multiply 40 by to get it to equal 100, we can divide 100 by 40, which gives us 2.5. The next step is to multiply both the numerator and denominator by 2.5 to give us our equivalent fraction. We know that the denominator of the fraction will be 100, so we only need to work out what 2.5 multiplied by 27 is. The easiest way to multiply by 2.5 is to split 2.5 up; we can multiply 27 by 2 (which is the same as doubling) and multiply 27 by 0.5 (which is the same as halving). We will then add the outcomes up.
We then add the outcomes up.
The numerator of the fraction is 67.5, which means that the fraction becomes.
The next step is to convert the fraction into a percentage. We are able to do this by multiplying the fraction by 100.
The divide by 100 (from the fraction) and multiply by 100 will cancel one another out. This just leaves the numerator as the percentage. Therefore, 67.5% of the shots were on target.
Like I said before, we never usually give the numerator or denominators of fractions as decimals, but it is fine when working out percentages; just make sure that in any other situation with fractions, you do not have the numerator or the denominator of a fraction as a decimal. Also, when you are dealing with fractions in other sections of maths, you need to make sure that you give them in their simplest form and that there are no improper fractions (which is where the numerator is greater than the denominator).
Like I said before, we never usually give the numerator or denominators of fractions as decimals, but it is fine when working out percentages; just make sure that in any other situation with fractions, you do not have the numerator or the denominator of a fraction as a decimal. Also, when you are dealing with fractions in other sections of maths, you need to make sure that you give them in their simplest form and that there are no improper fractions (which is where the numerator is greater than the denominator).
Example 4
Express 12 as a percentage of 5.
The first step in answering this question is to write out the fraction. We are asked to express 12 as a percentage of 5. This means that the numerator of the fraction will be 12 and the denominator of the fraction will be 5. The fraction is shown below:
Express 12 as a percentage of 5.
The first step in answering this question is to write out the fraction. We are asked to express 12 as a percentage of 5. This means that the numerator of the fraction will be 12 and the denominator of the fraction will be 5. The fraction is shown below:
The next step is to make the denominator of the fraction 100. Currently, the denominator is 5 and we are able to make it 100 by multiplying by 20. We want to create equivalent fractions, and this means that we need to multiply both the numerator and the denominator of the fraction by 20.
The final step is to convert the fraction into a percentage, which we are able to do by multiplying the fraction by 100.
The divide by 100 (from the fraction) and the multiply by 100 cancel each other out to just leave the numerator. Therefore, 12 as a percentage of 5 is 240%.