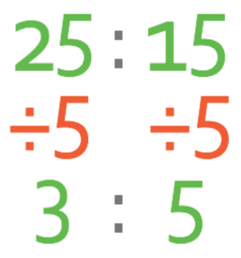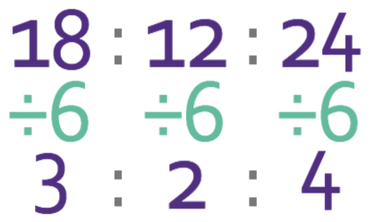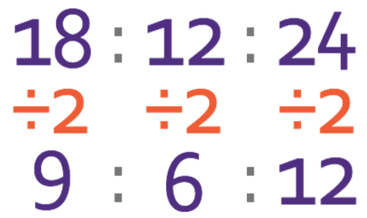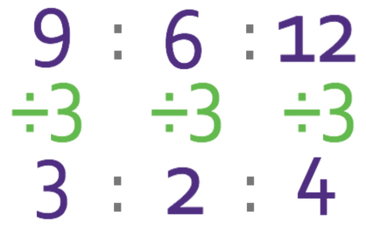Back to OCR Ratio (F) Home
3.3 A) Introduction & Simplifying Ratio – Part 1
3.3 A) Introduction & Simplifying Ratio – Part 1
A ratio shows the relative sizes of 2 or more values. Ratios are usually written with “:” between the numbers. The numbers in a ratio can be whole numbers, fractions, decimals or percentages.
For example, we can give the ratio of apples to bananas in the following fruit bowl.
For example, we can give the ratio of apples to bananas in the following fruit bowl.
From the above fruit bowl, we can see that the ratio between apples and bananas is 2 : 3. This means that for every two apples, there will be 3 bananas.
Simplifying Ratios – Part 1
Ratios are usually given in their simplest form. We can simplify ratios by finding the highest common factor between all of the terms in the ratio and dividing all of the terms by the common factor.
Ratios are usually given in their simplest form. We can simplify ratios by finding the highest common factor between all of the terms in the ratio and dividing all of the terms by the common factor.
Example 1
Simplify the following ratio:
Simplify the following ratio:
Both of the terms in the ratio above have a factor of 5 and 5 is the highest common factor. We can divide the first and second term by 5, which gives us:
There are no more common factors between these two terms, which means that the ratio is in its simplest form.
If we were given a ratio that had more than two terms, the method used to simplify the ratio would be the same; we would find the highest common factor between all of the terms in the ratio and divide by that factor.
If we were given a ratio that had more than two terms, the method used to simplify the ratio would be the same; we would find the highest common factor between all of the terms in the ratio and divide by that factor.
Example 2
Simplify the following ratio:
Simplify the following ratio:
The common factor in the 3 terms is 6. Therefore, we can divide all of the terms by 6.
If you are unsure what the highest common factor is between all of the terms in the ratio, you can divide all of the terms in the ratio by any common factor. You must then check the result to see if there are any more common factor between all of the terms in the ratio and divide by any that you find. You continue this process until there are no other common factors that you can divide by. For example, in the above ratio, we could have divided by 2.
The ratio above has a common factor of 3, so we can divide the terms by 3.
We still get the same answer as before.