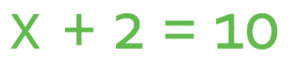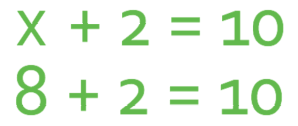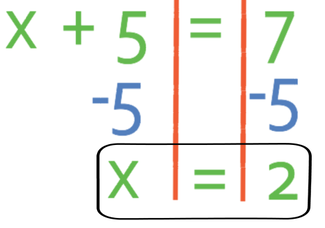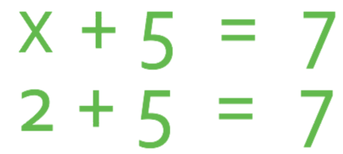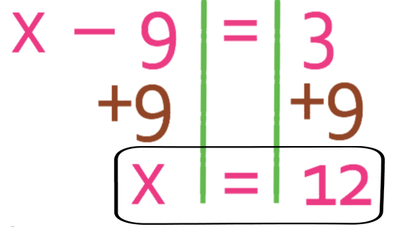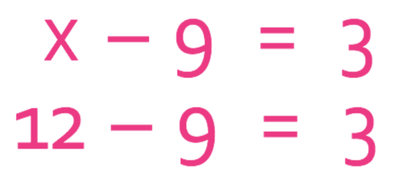Back to OCR Linear Equations (H) Home
2.2 A) Linear Equations: Addition & Subtraction
2.2 A) Linear Equations: Addition & Subtraction
An equation is a statement that has an equals sign in it. For example:
Equations display that two expressions are equal to one another. From the above equation, we can see that the expression “x + 2” is equal to 10.
We can solve equations to find the value or values for an unknown that results in the two expressions being equal to one another. The value for x in the above equation is 8 and we can prove that this is the case by subbing in x as 8.
We can solve equations to find the value or values for an unknown that results in the two expressions being equal to one another. The value for x in the above equation is 8 and we can prove that this is the case by subbing in x as 8.
This is an equation and not an identity because the equation above only holds when x is 8. An identity is a pair of expressions that hold whatever values are subbed in; if we were to sub in x as 3, the left side of the equation would be 5 (x + 2; 3 + 2), which is not equal to 10. The symbol for an identity is a ≡.
Throughout this section and the next sections, we are going to be looking at solving a variety of different types of linear equations. The highest power of an unknown in a linear equation is 1; there are no squared or cubed terms. The questions will start off fairly straightforward, but it is definitely worth going through them as the harder questions build on the methods that we will look at in the simpler questions.
Throughout this section and the next sections, we are going to be looking at solving a variety of different types of linear equations. The highest power of an unknown in a linear equation is 1; there are no squared or cubed terms. The questions will start off fairly straightforward, but it is definitely worth going through them as the harder questions build on the methods that we will look at in the simpler questions.
Adding & Subtracting
Example 1
Find the value of x in the equation below.
Example 1
Find the value of x in the equation below.
Whenever we are solving equations, we need to make sure that we do the same operations on both sides of the equals sign; whatever we do to one side must also be done on the other side. Therefore, it is a good idea to draw a wall going down the equals sign. This helps to ensure that what we do to one side, we also do to the other side. Also, it makes our working tidier and easier to follow.
When we are solving equations, it is a good idea to know what you are aiming for. The end result of the question is to find the value of x (x = “something”). Therefore, all of the operations that we do in this question are to get to this final outcome.
To do this we need to have all of the x’s on one side and the numbers on the other side. There is an x on the left side of the equation and no x’s on the right side of the equation. Therefore, it makes sense to have the left side of the equation as the side that has x terms, and the right side of the equation the side that has numbers. This means that we need to move the +5 that is currently on the left side of the equation to the right. We are able to do this by doing the opposite to both sides of the equation. The opposite of adding 5 is taking 5; therefore, we take 5 from both sides of the equation.
To do this we need to have all of the x’s on one side and the numbers on the other side. There is an x on the left side of the equation and no x’s on the right side of the equation. Therefore, it makes sense to have the left side of the equation as the side that has x terms, and the right side of the equation the side that has numbers. This means that we need to move the +5 that is currently on the left side of the equation to the right. We are able to do this by doing the opposite to both sides of the equation. The opposite of adding 5 is taking 5; therefore, we take 5 from both sides of the equation.
Subtracting 5 from both sides gives us the answer to the question, which is x = 2. We can check our answer by subbing x as 2 into the equation.
This equation works, which means that we have found the correct value for x; x is 2.
It is worth checking whether the value for the unknown does work in the equation because if the value does not work, it tells us that we have got the wrong answer.
It is worth checking whether the value for the unknown does work in the equation because if the value does not work, it tells us that we have got the wrong answer.
Example 2
Find the value of x.
Find the value of x.
I am going to set out the question in exactly the same way as before with a wall going down the equals sign. We then need to get all of the x’s on one side and the numbers on the other side. To do this, we need to move the - 9 from the left side of the equation to the right side. This is done by doing the opposite to both sides of the equation; the opposite of - 9 is + 9, so we add 9 to both sides of the equation.
This results in the value for x being 12. Like before, we can check whether this value for x is correct by subbing in 12 for x into the equation.
The equation above works, which means that x is 12.