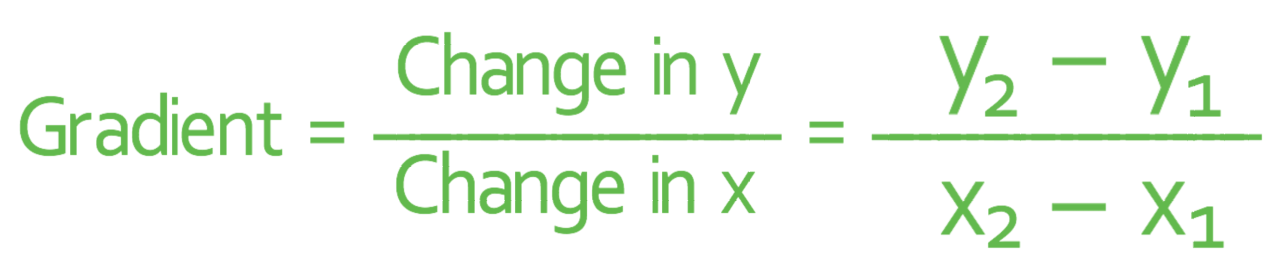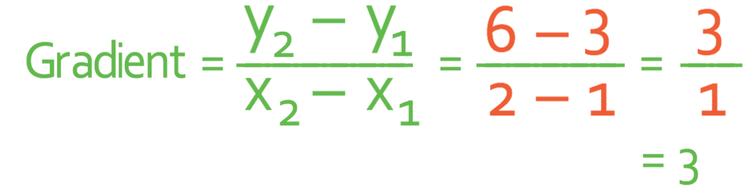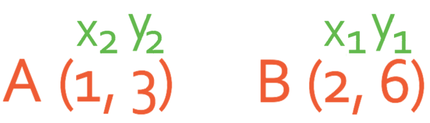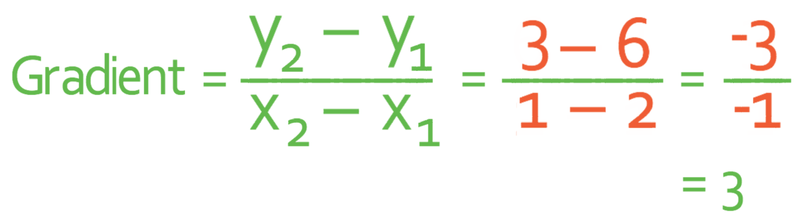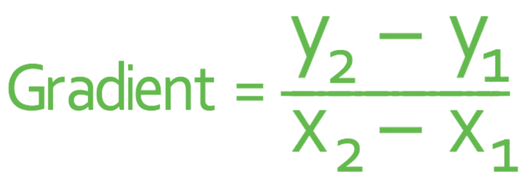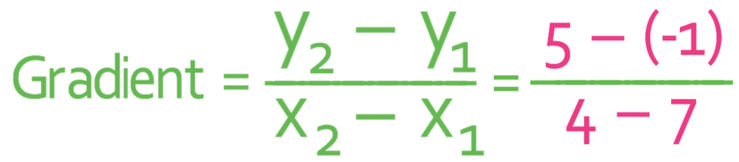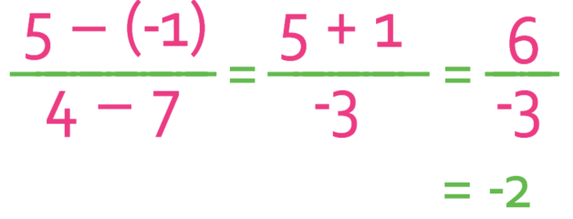2.5 G) Finding the Gradient
The gradient of a line is the slope of the line. It is the value of m when we have the equation for a line in the form y = mx + c. An upwards sloping line will have a positive gradient and a downwards sloping line will have a negative gradient.
If we have two points that lie on a line (or we can read two points from a graph that has the line plotted on), we can work out the gradient of a line by using the following formula:
Another way to remember how to work out the gradient of a line is to remember the gradient as “rise over run”; the rise is the change in y and the run is the change in x.
Example 1
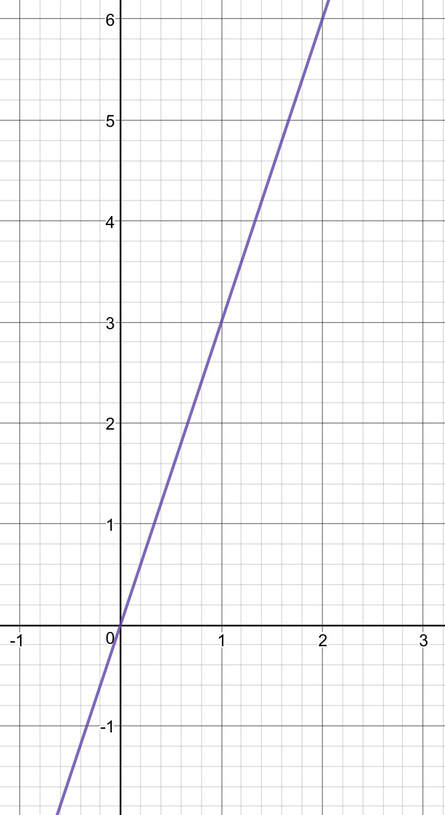
Find the gradient of the line on the graph below.
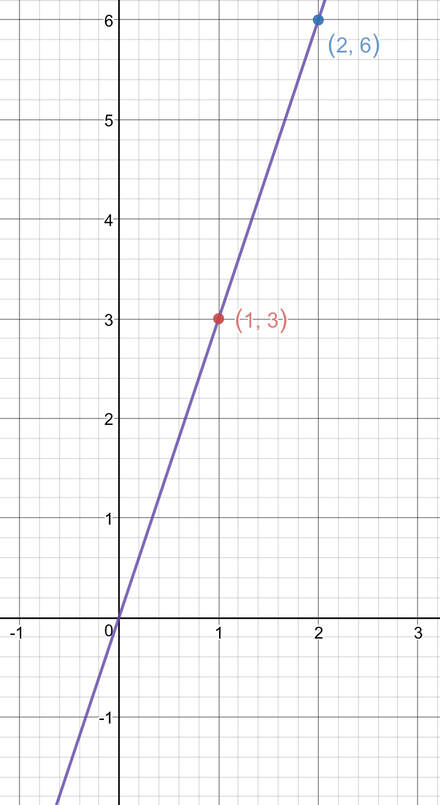
In order to work out the gradient of a line, we need to have two points that lie on the line. We are not given two points, but we are able to choose two points on the line and sub them into the formula above. We are able to choose any points on the line. This is because the line is straight, which means that the gradient of the line will be the same throughout the whole line, thus meaning that it does not matter what points we sub into the formula. However, whenever we are choosing points, make sure that you choose points that are easy to read off; choose coordinates that are on the grid lines and coordinates where the x and y values are integers. The two points that I have chosen are on the graph below.
The two points are A, which has the coordinates (1, 3) and B, which has the coordinates (2, 6). The next step is to assign one of the points as 1 meaning that the coordinates are x1 and y1, and the other point as 2 meaning that the coordinates are x2 and y2. It does not matter which point I choose as 1 and 2 (I will show this later by swapping the points).
I am going to choose point A as 1 and point B as 2. We now label the x and y values up for each of the points.
The next step is to sub the values into the formula to work out the gradient.
Therefore, the gradient is 3. This means that as x increases by 1, the value for y increases by 3.
Earlier I mentioned that it does not matter which point I label as 1 and 2. I am now going to label point A as 2 and point B as 1. The labelled up coordinates are shown below.
We can now sub these values into the gradient formula to find the gradient.
This tells us that the gradient of the line is 3, which is exactly the same gradient that we got when the coordinates were labelled the other way around.
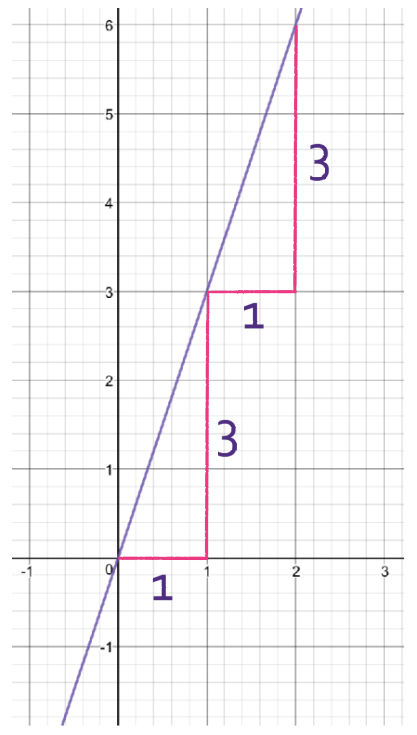
A second way that we can work out the gradient of a line when we are given a graph is to create little triangles where the change in x is 1. When the change in x is 1, the change in y will be the gradient.
From the triangle above, we can see that as x increases by 1, the value of y increases by 3. Therefore, the gradient for this line is 3.
This method is a very quick method to find the gradient when we are given the line on a graph. However, we will be unable to use this method if we were just given two points that lie on the line.
The points (7, -1) and (4, 5) lie on a line. What is the gradient of the line?
To find the gradient of the line, we are going to be using the formula below.
In order to use this formula, we need to have one of the points as point 1 (with the values x1 and y1) and the other point as point 2 (with the values x2 and y2). I am going to have point 1 as (7, -1) and point 2 as (4, 5). The labelled up points are shown below:
When we are using the gradient formula, we need to be very careful with the signs. I think that is best to use brackets around negative values; we will have brackets around the -1. The brackets ensure that you do not forget the signs.
The taking of a negative value results in us adding the number. This means that the – (-1) becomes +1.
Therefore, the gradient of the line is -2.