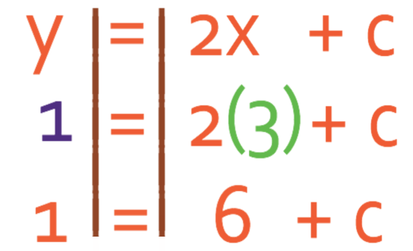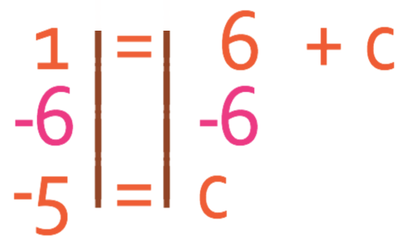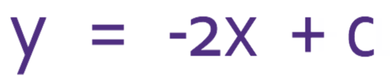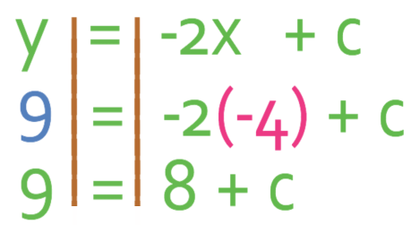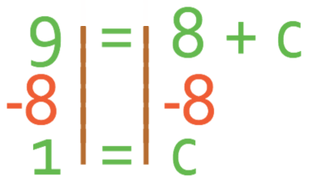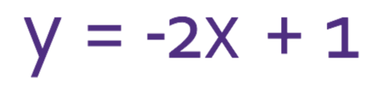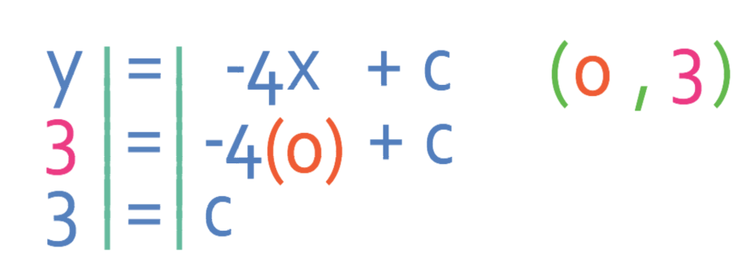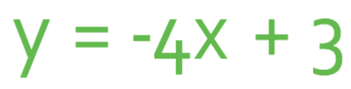Back to OCR Linear Graphs (H) Home
2.5 J) Finding the Equation of a Line – Gradient & a Point
2.5 J) Finding the Equation of a Line – Gradient & a Point
There are two situations where we may be asked to find the equation for a line in an exam. These two situations are:
- We are given the gradient of the line and a point that is on the line
- We are given two points that lie on the line
1) Gradient and One Point
The first case is where we are given the gradient of a line and a point that lies on the line. We know that linear lines have the equation y = mx + c, where m is the gradient and c is the y intercept. In the first case, we are given the gradient of the line, which is m. This means that we only need to find the value of c to find the equation of the line. We can find the value of c by subbing the x and y coordinates for the point that we are given. By subbing in these values, c will be the only unknown in the equation, thus meaning that we can find its value.
The first case is where we are given the gradient of a line and a point that lies on the line. We know that linear lines have the equation y = mx + c, where m is the gradient and c is the y intercept. In the first case, we are given the gradient of the line, which is m. This means that we only need to find the value of c to find the equation of the line. We can find the value of c by subbing the x and y coordinates for the point that we are given. By subbing in these values, c will be the only unknown in the equation, thus meaning that we can find its value.
Example 1
A line has a gradient of 2 and passes through the point (3, 1). What is the equation of the line?
The question gives us the gradient of the line, which is 2. This means that m in the generic formula of a linear line is 2. Therefore, we know that the line is going to be y = 2x + c.
A line has a gradient of 2 and passes through the point (3, 1). What is the equation of the line?
The question gives us the gradient of the line, which is 2. This means that m in the generic formula of a linear line is 2. Therefore, we know that the line is going to be y = 2x + c.
The next step is to find the value of c and we do this by subbing in the x and y values from the coordinates into the question. The coordinate that we were given was (3, 1), so we sub in x as 3 and y as 2 into the equation y = 2x + c. We then solve to find the value of c.
In order to find the value of c, we need to move the 6 from the right side of the equation to the left. We are able to this by taking 6 from both sides of the equation.
This tells us that c is -5. We are now able to replace c in the first equation with -5. This means that the equation for the line is:
Example 2
A line has a gradient of -2 and passes through the point (-4, 9). What is the equation of the line?
The question tells us that the gradient of the line is -2. This means that m is -2 and we know that the equation of the line can be written as y = -2x + c.
A line has a gradient of -2 and passes through the point (-4, 9). What is the equation of the line?
The question tells us that the gradient of the line is -2. This means that m is -2 and we know that the equation of the line can be written as y = -2x + c.
The next step is to find the value of c and we do this by subbing in the values for x and y from the coordinates that we are given; the coordinates are (-4, 9), which means that we sub in x as -4 and y as 9 to find c.
When we multiply a negative by a negative, we get a positive. This means that -2 x -4 is 8.
We find the value of c by moving the 8 from the right side of the equation to the left. We are able to do this by moving 8 from both sides of the equation.
We find the value of c by moving the 8 from the right side of the equation to the left. We are able to do this by moving 8 from both sides of the equation.
The value of c is 1, which means that the equation for the line is:
Example 3 – Given the Graph
It may be the case that you are given a graph and the gradient of a line. If this is the case, we find the value of c by looking for the y intercept (the y value for where the line passes through the y axis).
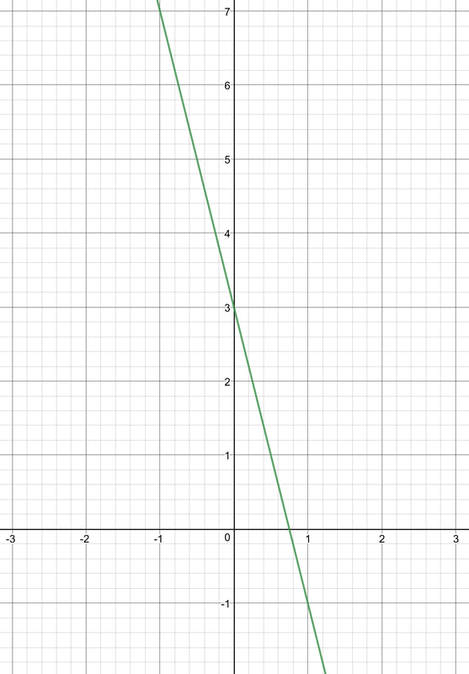
For example, we are given the line below and told that the gradient is -4. What is the equation of the line?
It may be the case that you are given a graph and the gradient of a line. If this is the case, we find the value of c by looking for the y intercept (the y value for where the line passes through the y axis).
For example, we are given the line below and told that the gradient is -4. What is the equation of the line?
The question tells us that the gradient of the line is -4, which means that m is -4. From the sketch, we can see that the line passes through the y axis when y is 3. This means that the value of c in the standard form for a linear line is 3. Therefore, the equation of the line is y = -4x + 3.
Another way that we could have found an equation for this line is to choose a point on the line and sub the x and y values for the coordinate into the equation of the line with the value of m subbed in. We were told in the question the gradient of the line is -4, and this means that m is -4. Therefore, the equation of the line is y = -4x + c, where c is an unknown. We can find the value of c by subbing in the x and y values from a point that lies on the line. Any point on the line will work for this. I am going to use the y intercept point, which has the coordinates (0, 3). This means that I will be subbing x as 0 and y as 3 into the equation y = -4x + c. We then solve to find the value of c.
Another way that we could have found an equation for this line is to choose a point on the line and sub the x and y values for the coordinate into the equation of the line with the value of m subbed in. We were told in the question the gradient of the line is -4, and this means that m is -4. Therefore, the equation of the line is y = -4x + c, where c is an unknown. We can find the value of c by subbing in the x and y values from a point that lies on the line. Any point on the line will work for this. I am going to use the y intercept point, which has the coordinates (0, 3). This means that I will be subbing x as 0 and y as 3 into the equation y = -4x + c. We then solve to find the value of c.
Therefore, the value of c is 3. This means that the equation of the line is y = -4x + 3 and this is the same equation that we found using the other method.