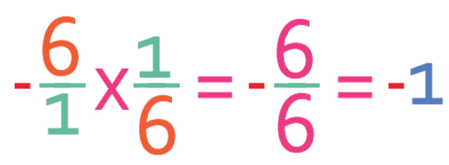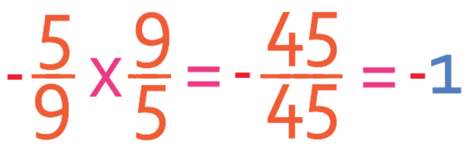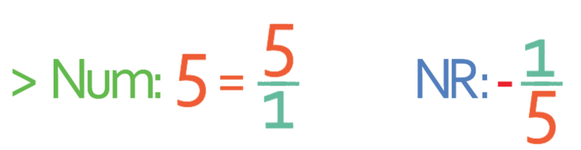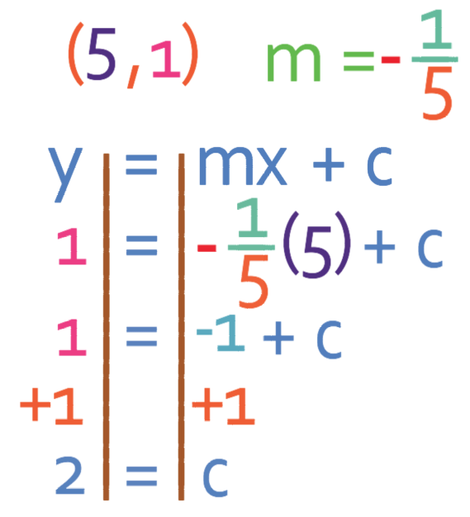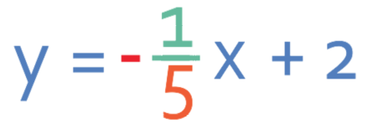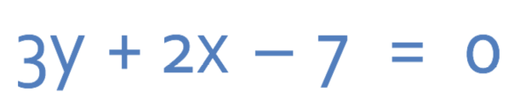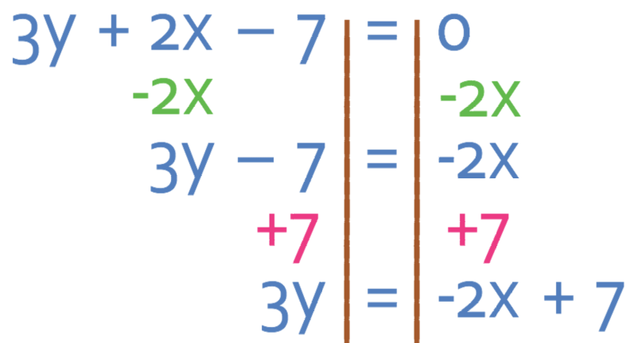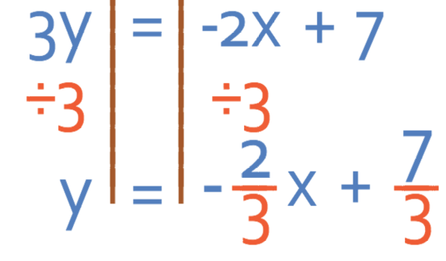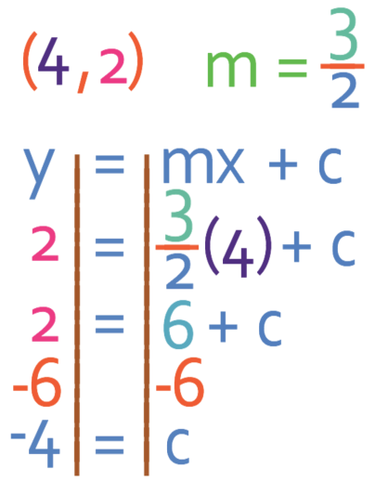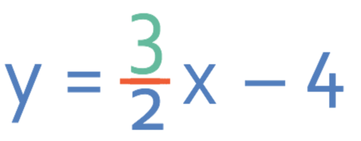2.5 L) Perpendicular Lines
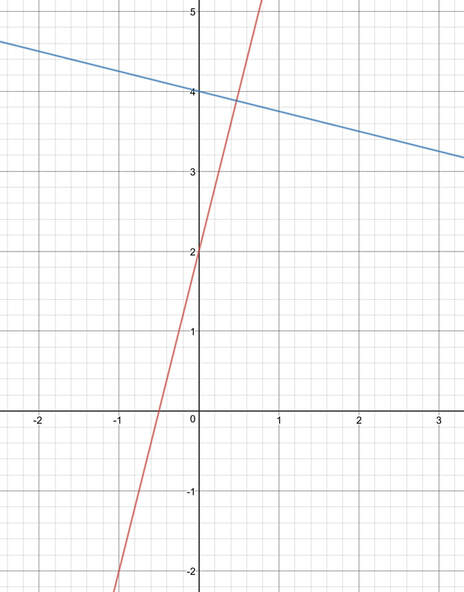
Perpendicular lines are lines that meet at a right angle. For example, the two lines on the graph below are perpendicular because they cross at a right angle.
The product of the gradients of two lines that are perpendicular to each other is -1 (product means the multiplication). We will see that this is the case later.
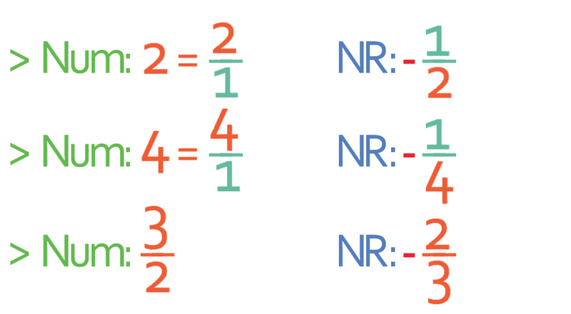
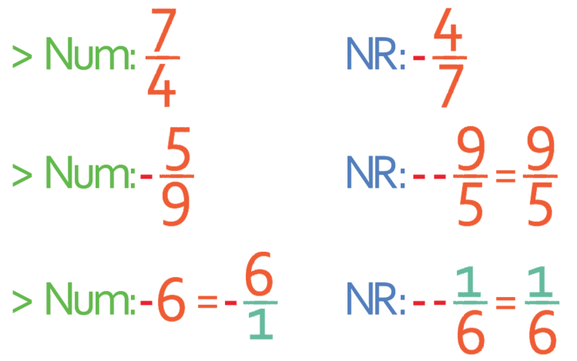
It may be the case that we are given the gradient of a line (line 1) and asked to find what the gradient of another line (line 2) that is perpendicular to the first line (line 1). We do this by finding the negative reciprocal of the gradient of line 1. We find the negative reciprocal of a number by flipping a fraction (the numerator is now the denominator and the denominator is now the numerator) and placing a minus in front of it. If we are finding the negative reciprocal of a whole number (such as 5), you may find it easier to place the whole number over 1 and then flip the fraction and add a minus sign. Here are some numbers and their negative reciprocals:
Earlier, I mentioned that the product of the gradients of two lines that are perpendicular to each other is -1. We know that lines that are perpendicular to one another will have gradient’s that are the negative reciprocal of one another. This means that the products of all of the pairs above should be -1. Let’s check the last one, which is 6 and -1/6. When we multiply fractions, we multiply straight across; we multiply both of the numerators, and we multiply both of the denominators.
The product of these two gradients is -1.
Let’s now check -5/9 and 9/5.
This also has a product of -1.
Find the equation of the line (line A) that is perpendicular to y = 5x + 4 (line B) and passes through the point (5, 1).
In order to find the gradient of line A, we must first find what the gradient is of line B. Line B is already in the form y = mx + c. This means that the gradient of line B is the value for m, which is 5. The next step is to find the negative reciprocal of the gradient of line B. The negative reciprocal of 5 is -1/5. Therefore, the gradient of line A (perpendicular to B) is -1/5.
This means that line A will have the equation y = -1/5x + c. We can find the value of c by using the point that line A passes through, which is (5, 1). Therefore, we find c by subbing x as 5 and y as 1.
The value of c is 2. Therefore, line A has the equation:
A line C is perpendicular to line D. Line D has the equation 3y + 2x – 7 = 0. Line C passes through the point (4, 2). What is the equation for line C?
We are told that line C is perpendicular to line D. Therefore, the first step in answering this question is to find what the gradient is of line D (as we are given the equation of line D). After we have the gradient of line D, we can find the negative reciprocal and that will be the gradient of line C.
Let’s find the gradient of line D first and the best way to do this is to get the equation into the form y = mx + c. The equation for line D is given below:
In order to get this line into the form y = mx + c, we need to move the 2x and the -7 across from the left side of the equation to the right. We are able to do this by doing the opposite to both sides of the equation.
The next step is to divide both sides by 3 and this is because we want to find what y is and not what 3y is.
We now have the line in the form of y = mx + c, which means that we can easily find the gradient of the line. The gradient of line D is -2/3. As line C is perpendicular to line D, the gradient for line C will be the negative reciprocal of the gradient for line D. To find the negative reciprocal, we flip the fraction and add a minus sign.
Therefore, the gradient for line C is 3/2, which means that line C has the equation y = 3/2x + c. To find the value of c, we sub in the coordinates that we are given in the question. We are told that line C goes through the point (4, 2), so we sub in x as 4 and y in as 2.
Therefore, the equation for line C is: