Back to OCR Direct & Inverse Proportion (H) Home
3.1 G) Direct & Inverse Proportion Tables
3.1 G) Direct & Inverse Proportion Tables
Sometimes we will be told that two variables are in direct or inverse proportion to each. We will then be given a table with some gaps in and asked to find out what the missing values are. We are going to look at answering these types of questions in this section.
Example 1
x is directly proportional to y.
Fill in the missing values in the table.
x is directly proportional to y.
Fill in the missing values in the table.
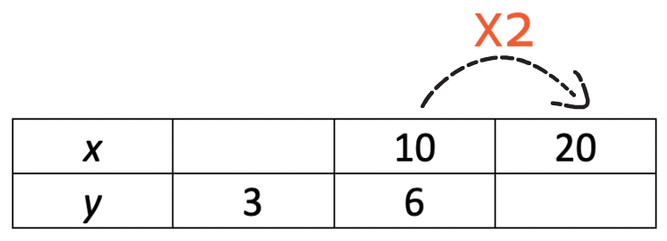
Whenever we are given a table of values for direct and inverse proportion, we will always be given a pair of values for x and y. For this table, the pair of values are x as 10 and y as 6.
The question tells us that x and y are in direct proportion to one another. This means that the variables move in the same direct as each other; if one variable was to increase, so too would the other variable. Also, if one variable was to decrease, so too would the other variable. The increase or decrease would be in the same proportion. For example, if one variable was to double, the other variable would also double (and if one was to halve, so too would the other variable).
Therefore, the easier way to answers these types of questions is to work out what we multiple or divide by to obtain the different values in the table. I am going to work out the bottom right value first. We work it out by looking at what we multiply 10 by to obtain 20, which is 2.
The question tells us that x and y are in direct proportion to one another. This means that the variables move in the same direct as each other; if one variable was to increase, so too would the other variable. Also, if one variable was to decrease, so too would the other variable. The increase or decrease would be in the same proportion. For example, if one variable was to double, the other variable would also double (and if one was to halve, so too would the other variable).
Therefore, the easier way to answers these types of questions is to work out what we multiple or divide by to obtain the different values in the table. I am going to work out the bottom right value first. We work it out by looking at what we multiply 10 by to obtain 20, which is 2.
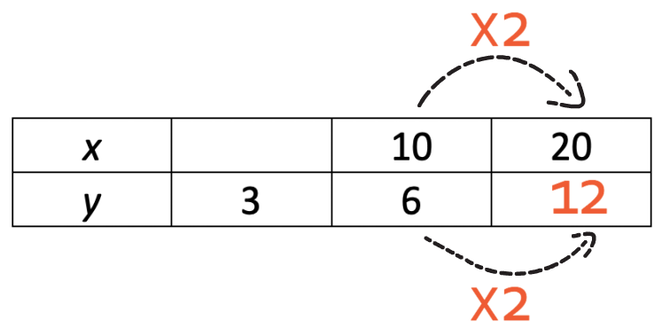
These variables are in direct proportion, which means that if x doubles (x2), y will also double. Therefore, we multiply 6 by 2 to get 12.
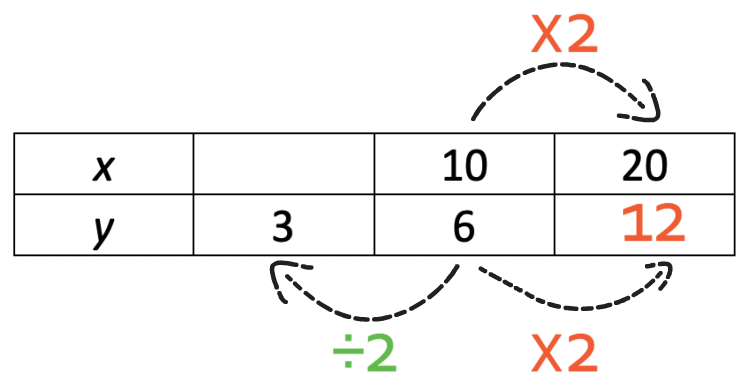
I am now going to work out the top left value. To go from 6 to 3, we divide by 2.
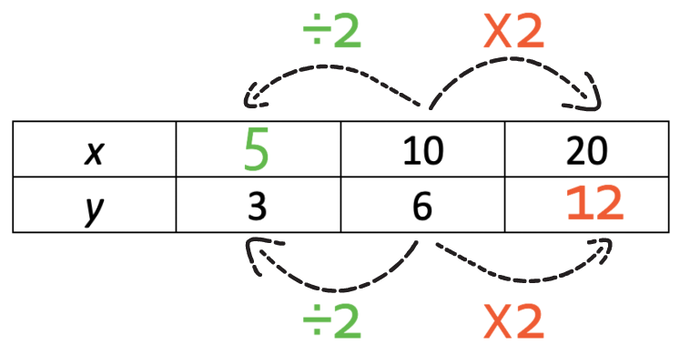
Therefore, we obtain the x value by dividing 10 by 2, which gives 5.
The table is now complete.
We could have answered this question by using the general equation for direct proportion, which is y = kx. We would then sub in x as 10 and y as 6 to find the value of k in the general equation for direct proportion. We would then sub the respective x or y values in to find the missing values in the table. This method would give exactly the same answers that we obtained, but it would have taken a lot longer and there is a greater chance of making a mistake as there are more steps. Therefore, it is best to use the method that I have just gone through.
We could have answered this question by using the general equation for direct proportion, which is y = kx. We would then sub in x as 10 and y as 6 to find the value of k in the general equation for direct proportion. We would then sub the respective x or y values in to find the missing values in the table. This method would give exactly the same answers that we obtained, but it would have taken a lot longer and there is a greater chance of making a mistake as there are more steps. Therefore, it is best to use the method that I have just gone through.
Example 2
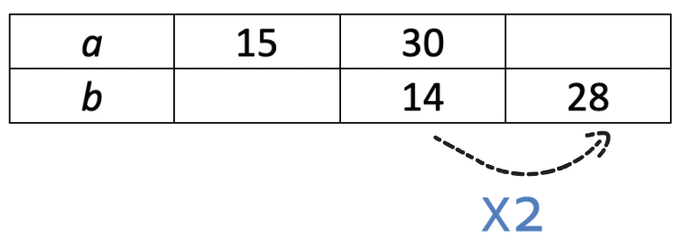
a is directly proportional to b.
Fill in the missing values in the table.
a is directly proportional to b.
Fill in the missing values in the table.
These variables are in direct proportion, which means that the variables will move in the same direction. Therefore, whatever we multiply (or divide) one variable by, we do the same for the other variable. If we multiplied a by 2, we would multiply b by 2 as well.
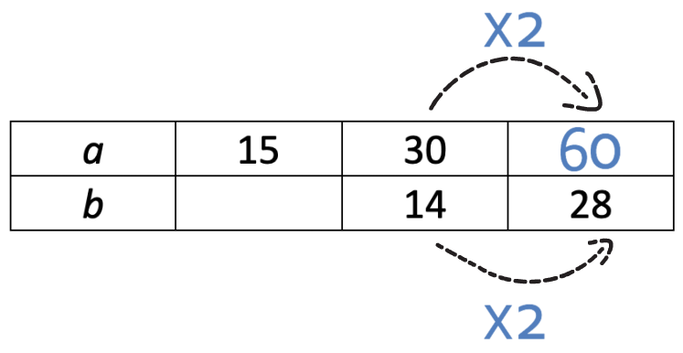
I am going to find the top right value first. In order to go from 14 to 28, we multiply by 2.
I am going to find the top right value first. In order to go from 14 to 28, we multiply by 2.
Therefore, we multiply 30 by 2, which gives us 60.
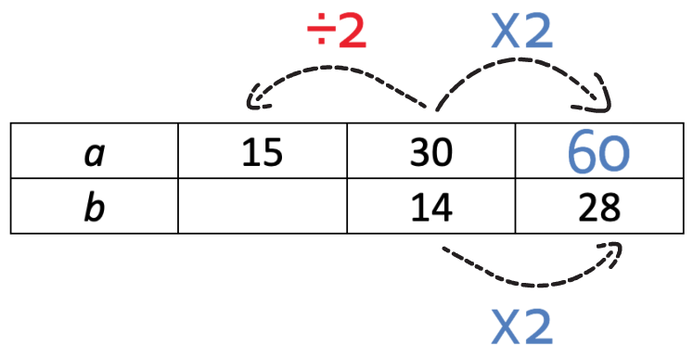
I am now going to find the bottom left value. In order to go from 30 to 15, we divide by 2.
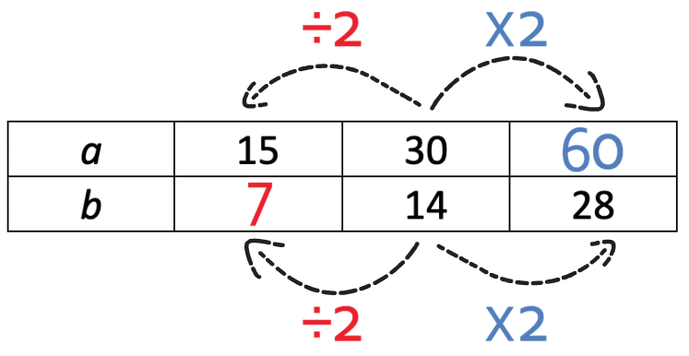
Therefore, we divide 14 by 2, which gives us 7.
The table is now completed.
Example 3
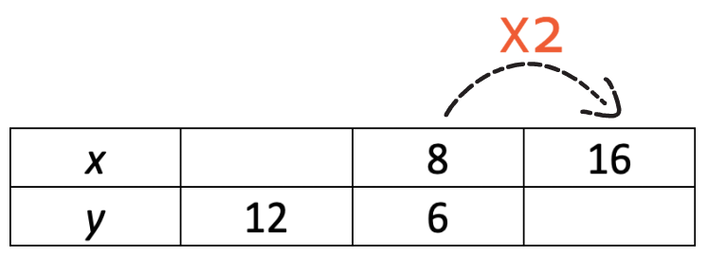
x is inversely proportional to y.
Fill in the missing values in the table.
x is inversely proportional to y.
Fill in the missing values in the table.
Variables that are in inverse proportion move in opposite directions. If one variable was to increase, the other variable would decrease (and vice versa). We work out the values in the table in pretty much the same way as direct proportion. The only difference is that we perform the opposite operation. For example, if the x value was multiplied by 2 (the x value doubled), the y value would be divided by 2 (it would be halved).
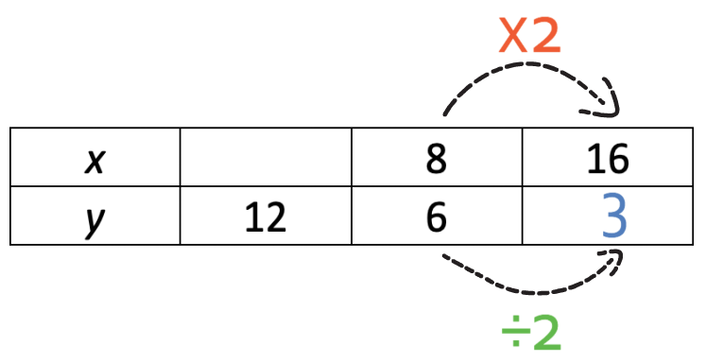
I am going to work out the bottom right value. In order to go from 8 to 16, we multiply by 2.
I am going to work out the bottom right value. In order to go from 8 to 16, we multiply by 2.
These variables are in inverse proportion, which means that they move in opposite directions. As the x value has been multiplied by 2, the y value will be divided by 2. Therefore, we divide 6 by 2, which gives 3.
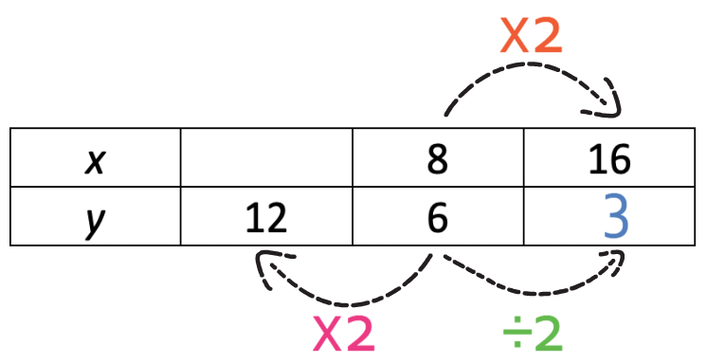
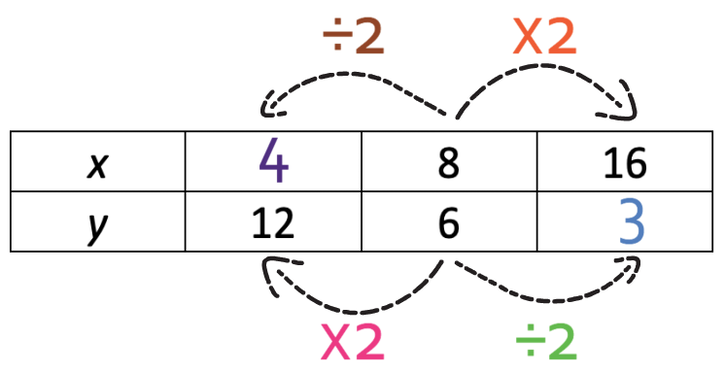
I am now going to find the top left value. In order to go from 6 to 12, we multiply by 2.
These variables are in inverse proportion, which means that they move in the opposite directions. Therefore, we obtain the top left value by doing the opposite; the opposite of multiplying by 2 is dividing by 2. This means that we divide 8 by 2, which is 4.
The table is now completed.
Example 4
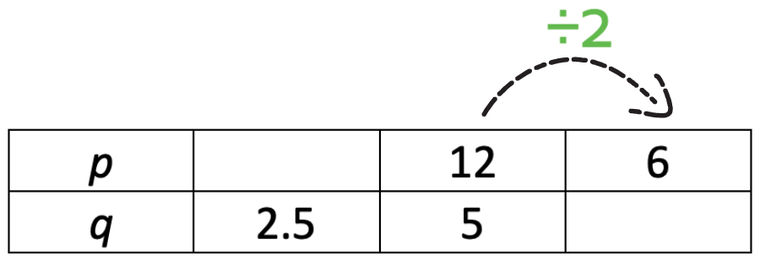
p is inversely proportional to q.
Fill in the missing values in the table.
p is inversely proportional to q.
Fill in the missing values in the table.
These variables are in inverse proportion, which means that they will move in opposite directions.
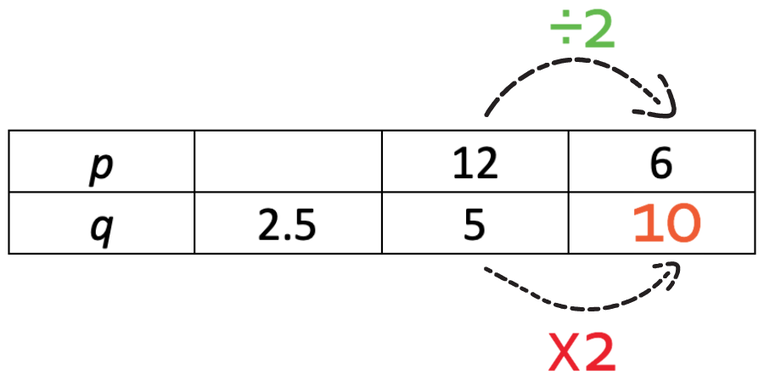
I am going to find the bottom right value first. In order to go from 12 to 6, we divide by 2.
I am going to find the bottom right value first. In order to go from 12 to 6, we divide by 2.
These variables are in inverse proportion, which means that the variables move in opposite directions. This means that if p has been divided by 2, q will be multiplied by 2. Therefore, we multiply 5 by 2, which is 10.
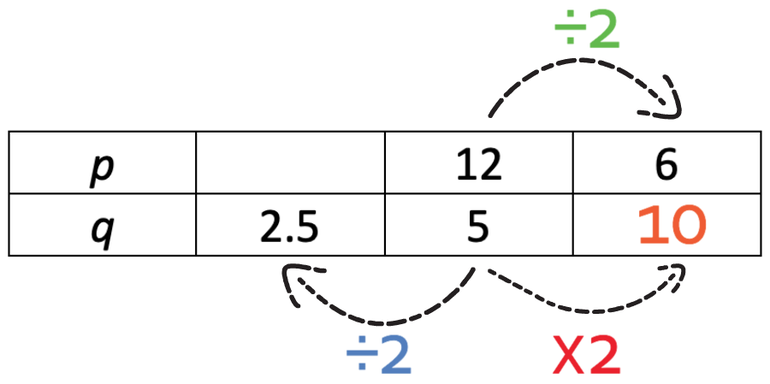
I am now going to find the top left value. In order to go from 5 to 2.5, we divide by 2.
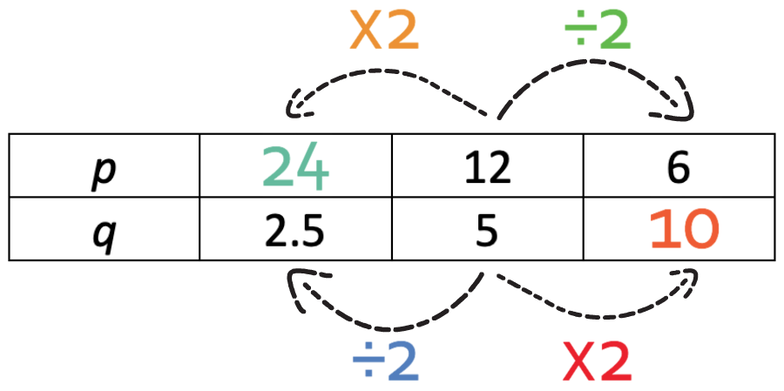
These variables are in inverse proportions, which means that the variables will move in opposite directions. This means that if q has been divided by 2, p will be multiplied by 2. Therefore, we multiply 12 by 2, which is 24.
The table is now completed.
End Note
Questions like this are fairly straight forward providing that you remember the rules for direct and inverse proportion. The rules are:
Providing that you remember these rules, you should have no issues with answering these types of questions. It may be worth getting a direct proportion table example and an inverse proportion table example down on a revision card.
Questions like this are fairly straight forward providing that you remember the rules for direct and inverse proportion. The rules are:
- Variables that are directly proportional to one another move in the same direction. This means that we obtain the missing values by carrying out the same operation. If one variable has been multiplied, we multiply the other variable by the same value. If one variable has been divided, we divide the other variable by the same value.
- Variables that are inversely proportional to one another move in opposite directions. This means that we obtain the missing values by carrying out the opposite operation. If one variable has been multiplied, we divide the other variable by the same value. If one variable has been divided, we multiply the other variable by the same value.
Providing that you remember these rules, you should have no issues with answering these types of questions. It may be worth getting a direct proportion table example and an inverse proportion table example down on a revision card.