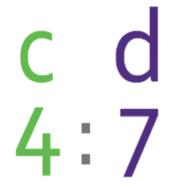Back to OCR Ratio (H) Home
3.3 I) Fractions from Ratios – Part 2
3.3 I) Fractions from Ratios – Part 2
In the previous section, we were looking at questions whereby we were asked to work out the fraction of the total that a component in the ratio represented (click here to be taken back to the previous section).
In this section, we are going to be working out what one component of the ratio is as a fraction of another component in the ratio. I will go through how we answer these types of questions with an example.
In this section, we are going to be working out what one component of the ratio is as a fraction of another component in the ratio. I will go through how we answer these types of questions with an example.
Example 1
The ratio of a to b is:
The ratio of a to b is:
Find the following fractions (your answers can be left as improper fractions):
All of the subparts for this question contain the words “as a fraction of” and this means that we will answer all of the subparts of this question in the same way. The numerator of the fractions will be the number of parts for the component that appears before the “as a fraction of”. The denominator of the fraction will be the number of parts for the component that appears after the “as a fraction of”. This will all make more sense after we have gone through all of the subparts for this question.
Part 1
Part 1 asks us to work out a as a fraction of the total.
The numerator of the fraction will be the number of parts for the component that appears before the “as a fraction of”. a is before the “as a fraction of” and a has 3 parts in the ratio. This means that the numerator of the fraction is 3.
- a as a fraction of the total
- b as a fraction of the total
- a as a fraction of b
- b as a fraction of a
All of the subparts for this question contain the words “as a fraction of” and this means that we will answer all of the subparts of this question in the same way. The numerator of the fractions will be the number of parts for the component that appears before the “as a fraction of”. The denominator of the fraction will be the number of parts for the component that appears after the “as a fraction of”. This will all make more sense after we have gone through all of the subparts for this question.
Part 1
Part 1 asks us to work out a as a fraction of the total.
The numerator of the fraction will be the number of parts for the component that appears before the “as a fraction of”. a is before the “as a fraction of” and a has 3 parts in the ratio. This means that the numerator of the fraction is 3.
The denominator of the fraction will be the number of parts for the component that appears after the “as a fraction of”. The total appears after the “as a fraction of”, which means that the denominator of the fraction will be the total number of parts in the ratio. We work out the total number of parts in the ratio by adding up all of the parts for the different components; we add 3 and 5 to get 8 (3 + 5 = 8). This means that the denominator of the fraction is 8.
We now need to check whether our fraction can be simplified, which we do by looking for any common factors between the numerator and the denominator of the fraction. There are no common factors between 3 and 8, which means that this fraction is already in its simplest form.
Part 2
The second part asks us to work out b as a fraction of the total.
The numerator of the fraction will be the number of parts for the component that appears before the “as a fraction of”. b is before the “as a fraction of” and b has 5 parts in the ratio. This means that the numerator of the fraction is 5.
Part 2
The second part asks us to work out b as a fraction of the total.
The numerator of the fraction will be the number of parts for the component that appears before the “as a fraction of”. b is before the “as a fraction of” and b has 5 parts in the ratio. This means that the numerator of the fraction is 5.
The denominator of the fraction will be the number of parts for the component that appears after the “as a fraction of”. The total appears after the “as a fraction of”, which means that the denominator of the fraction will be the total number of parts in the ratio. We worked out in the previous subpart of the question that the total number of parts was 8 (3 + 5 = 8). Therefore, the denominator of the fraction is 8.
The final step is to check whether the fraction can be simplified. There are no common factors between 5 and 8, which means that the fraction above is in its simplest form.
Part 3
This part asks us to find a as a fraction of b.
The number of parts for the component before the “as a fraction of” will be the numerator of the fraction. This means that the number of parts that a has will be the numerator of this fraction. a has 3 parts in the ratio, so the numerator of the fraction is 3.
Part 3
This part asks us to find a as a fraction of b.
The number of parts for the component before the “as a fraction of” will be the numerator of the fraction. This means that the number of parts that a has will be the numerator of this fraction. a has 3 parts in the ratio, so the numerator of the fraction is 3.
The number of parts for the component after the “as a fraction of” will be the denominator of the fraction. This means that the number of parts that b has will be the denominator of the fraction. b has 5 parts in the ratio, which means that 5 will be the denominator of the fraction.
We now check whether the fraction can be simplified, which it can’t because there are no common factors between 3 and 5.
Part 4
The final part asks us to find b as a fraction of a.
The number of parts for the component before the “as a fraction of” will be the numerator. This means that the number of parts that b has will be the numerator of this fraction. b has 5 parts, so the numerator of the fraction is 5.
Part 4
The final part asks us to find b as a fraction of a.
The number of parts for the component before the “as a fraction of” will be the numerator. This means that the number of parts that b has will be the numerator of this fraction. b has 5 parts, so the numerator of the fraction is 5.
The number of parts for the component after the “as a fraction of” will be the denominator of the fraction. This means that the number of parts that a has will be the denominator of the fraction. a in the ratio has 3 parts, which means that 3 will be the denominator of the fraction.
We now check whether the fraction is in its simplest form. There are no common factors between 5 and 3, which means that this fraction is in its simplest form.
Example 2
The ratio of c to d is:
The ratio of c to d is:
Find the following fractions (your answers can be left as improper fractions):
Part 1
The first part asks us to find d as a fraction of c.
The numerator of the fraction will be the number of parts for the component before the “as a fraction of”. d is before the “as a fraction of”, and d in the ratio has 7 parts. This means that the numerator of the fraction is 7.
The denominator of the fraction will be the number of parts for the component after the “as a fraction of”. c is after the “as a fraction of”, and c in the ratio has 4 parts. This means that the denominator of the fraction is 4.
The fraction is:
- d as a fraction of c
- c as a fraction of d
- c as a fraction of the total
Part 1
The first part asks us to find d as a fraction of c.
The numerator of the fraction will be the number of parts for the component before the “as a fraction of”. d is before the “as a fraction of”, and d in the ratio has 7 parts. This means that the numerator of the fraction is 7.
The denominator of the fraction will be the number of parts for the component after the “as a fraction of”. c is after the “as a fraction of”, and c in the ratio has 4 parts. This means that the denominator of the fraction is 4.
The fraction is:
The final step is to check whether the fraction can be simplified. There are no common factors between 7 and 4, which means that this fraction is in its simplest form.
Part 2
The second part asks us to find c as a fraction of d.
The numerator of the fraction will be the number of parts for the component before the “as a fraction of”. c is before the “as a fraction of”, and c in the ratio has 4 parts. This means that the numerator of the fraction is 4.
The denominator of the fraction will be the number of parts for the component after the “as a fraction of”. d is after the “as a fraction of”, and d in the ratio has 7 parts. This means that the denominator of the fraction is 7.
The fraction is:
Part 2
The second part asks us to find c as a fraction of d.
The numerator of the fraction will be the number of parts for the component before the “as a fraction of”. c is before the “as a fraction of”, and c in the ratio has 4 parts. This means that the numerator of the fraction is 4.
The denominator of the fraction will be the number of parts for the component after the “as a fraction of”. d is after the “as a fraction of”, and d in the ratio has 7 parts. This means that the denominator of the fraction is 7.
The fraction is:
We now need to check whether the fraction can be simplified. There are no common factors between 4 and 7, which means that this fraction is in its simplest form.
Part 3
The final part asks us to find c as a fraction of the total.
The numerator of the fraction will be the number of parts for the component before the “as a fraction of”. c is before the “as a fraction of”, and c in the ratio has 4 parts. This means that the numerator of the fraction is 4.
The denominator of the fraction will be the number of parts for the component after the “as a fraction of”. The total is after the “as a fraction of”. We work out the total parts in the ratio by adding up all of the parts for the different components in the ratio; we add 4 and 7 to get 11 (4 + 7 = 11). This means that the denominator of the fraction is 11.
The fraction is:
Part 3
The final part asks us to find c as a fraction of the total.
The numerator of the fraction will be the number of parts for the component before the “as a fraction of”. c is before the “as a fraction of”, and c in the ratio has 4 parts. This means that the numerator of the fraction is 4.
The denominator of the fraction will be the number of parts for the component after the “as a fraction of”. The total is after the “as a fraction of”. We work out the total parts in the ratio by adding up all of the parts for the different components in the ratio; we add 4 and 7 to get 11 (4 + 7 = 11). This means that the denominator of the fraction is 11.
The fraction is:
The final step is to check whether the fraction can be simplified. There are no common factors between 4 and 11, which means that this fraction is in its simplest form.
End Note
Questions like this are fairly straight forward, but they do not appear that often, which means that the process in answering these types of questions is fairly easy to forget. Therefore, it is worth getting one of these examples down on a revision card.
Questions like this are fairly straight forward, but they do not appear that often, which means that the process in answering these types of questions is fairly easy to forget. Therefore, it is worth getting one of these examples down on a revision card.