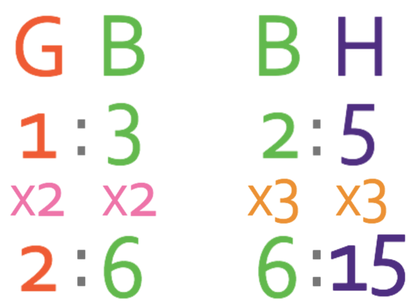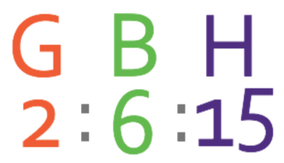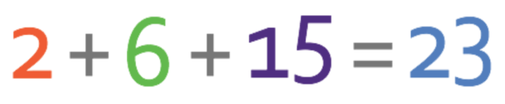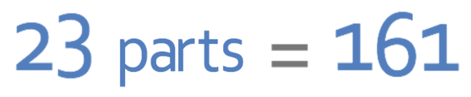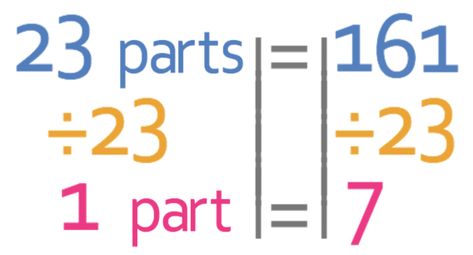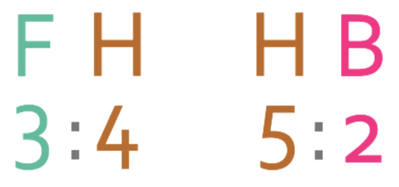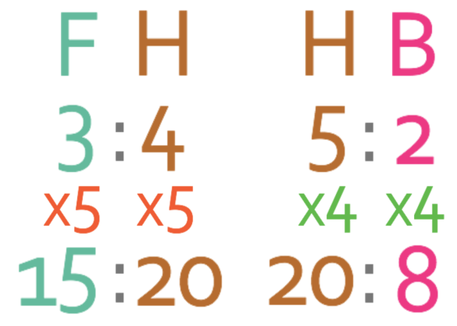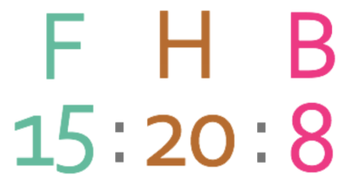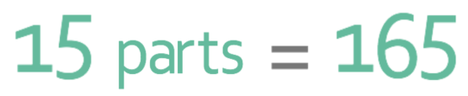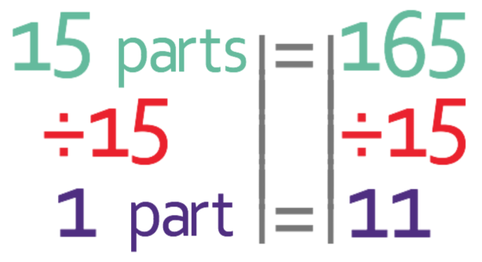Back to OCR Ratio (H) Home
3.3 J) Combing Ratios
3.3 J) Combing Ratios
Sometimes it will be the case that we are given two ratios and asked to combine the ratios to make one ratio. We are only able to combine ratios if one of the components is present in both of the ratios. If this is the case, we can combine the ratios by making the value for the component that appears in both of the ratios the same. We make the value for the component that appears in both of the ratios the lowest common multiple of the current values for that component in the two separate ratios. After we have made the values for the component that appears in both of the ratios the same, we can combine the ratios. This will all make more sense after we have looked at some examples.
Example 1
161 sweets are split between 3 different individuals; Gavin, Ben & Holly. The ratio of sweets between Gavin and Ben is 1 : 3. The ratio of sweets between Ben and Holly is 2 : 5. How many sweets does Ben get?
The best way to answer this question is to combine the ratios. The two ratios that we are given in the question are shown below; on the ratios below G is for Gavin, B is for Ben and H is for Holly.
161 sweets are split between 3 different individuals; Gavin, Ben & Holly. The ratio of sweets between Gavin and Ben is 1 : 3. The ratio of sweets between Ben and Holly is 2 : 5. How many sweets does Ben get?
The best way to answer this question is to combine the ratios. The two ratios that we are given in the question are shown below; on the ratios below G is for Gavin, B is for Ben and H is for Holly.
From looking at the ratios above, we notice that Ben appears in both ratios. We are able to combine the two ratios by making the value for Ben in both of the ratios the same. We make the value for Ben the lowest common multiple between the current values for Ben in the two ratios. Currently, Ben is 3 in the first ratio and 2 in the second ratio. The lowest common multiple for 3 and 2 is 6. Therefore, we make Ben 6 in both of the ratios.
We can make Ben 6 in the first ratio by multiplying both of the components in the first ratio by 2. And, we can make Ben 6 in the second ratio by multiplying both of the components in the second ratio by 3. The working is shown below.
We can make Ben 6 in the first ratio by multiplying both of the components in the first ratio by 2. And, we can make Ben 6 in the second ratio by multiplying both of the components in the second ratio by 3. The working is shown below.
We now have Ben as 6 in both of the ratios, which means that we are able to combine the ratios to get the ratio of sweets for Gavin, Ben and Holly as:
We now have the combined ratio and are in a good position to answer the question. We were told in the question that 161 sweets are shared between the 3 individuals. These 161 sweets is going to be equal to the total number of parts in the combined ratio. We work out the total number of parts in the combined ratio by adding the three components in the ratio together.
This tells us that the total number of parts in the ratio is 23. These 23 parts will be equal to the total number of sweets (which is 161) and this gives us the equation that is shown below:
We are able to find what 1 part in the ratio is equal to by dividing both sides of the equation by 23.
Therefore, 1 part in the combined ratio is 7 sweets.
The question asks us to work out the number of sweets that Ben gets. We can work this out by multiplying the number of parts that Ben has in the combined ratio by what 1 part in the combined ratio represents. Ben has 6 parts in the combined ratio and 1 part in the combined ratio is 7 sweets. The calculation for the number of sweets that Ben gets is shown below:
The question asks us to work out the number of sweets that Ben gets. We can work this out by multiplying the number of parts that Ben has in the combined ratio by what 1 part in the combined ratio represents. Ben has 6 parts in the combined ratio and 1 part in the combined ratio is 7 sweets. The calculation for the number of sweets that Ben gets is shown below:
This tells us that Ben gets 42 sweets.
Example 2
The ratio of flats to houses in a village is 3 : 4. The ratio of houses to bungalows in the same village is 5 : 2.
There are 165 flats. How many bungalows are there?
Before we start answering this question, I am going write both of the ratios out next to one another; F is for flats, H is for houses and B is for bungalows.
The ratio of flats to houses in a village is 3 : 4. The ratio of houses to bungalows in the same village is 5 : 2.
There are 165 flats. How many bungalows are there?
Before we start answering this question, I am going write both of the ratios out next to one another; F is for flats, H is for houses and B is for bungalows.
From looking at the above ratios, we can see that houses appears in both of the ratios. This means that we will be able to combine the two ratios to have one ratio that is for the number of flats to the number of houses to the number of bungalows.
In order to be able to combine the ratios, we need to make the value for the component that appears in both ratios the same. Houses appeared in both ratios, so we make the value for houses the same in both of the ratios. We make the value for houses the lowest common multiple between the two current values for houses in the ratio. Currently, houses is 4 in the first ratio and 5 in the second ratio. The lowest common multiple between 4 and 5 is 20. Therefore, we make houses 20 in both of the ratios.
We can make houses 20 in the first ratio by multiplying both of the components in the ratio by 5. And, we can make houses 20 in the second ratio by multiplying both of the components by 4. The working is shown below.
In order to be able to combine the ratios, we need to make the value for the component that appears in both ratios the same. Houses appeared in both ratios, so we make the value for houses the same in both of the ratios. We make the value for houses the lowest common multiple between the two current values for houses in the ratio. Currently, houses is 4 in the first ratio and 5 in the second ratio. The lowest common multiple between 4 and 5 is 20. Therefore, we make houses 20 in both of the ratios.
We can make houses 20 in the first ratio by multiplying both of the components in the ratio by 5. And, we can make houses 20 in the second ratio by multiplying both of the components by 4. The working is shown below.
We now have houses as 20 in both of the ratios, and this means that we are able to combine the two ratios to get the ratio of the number of flats to the number of houses to the number of bungalows. The ratio is:
We now have the combined ratio and are in a good position to answer the question. We were told in the question that there are 165 flats. In the combined ratio that we have just found, the flats are represented by 15 parts. These 15 parts must be equal to the 165 flats. We can create the following equation from this information:
We are able to find what 1 part represents by dividing both sides of the equation by 15.
This tells us that 1 part in the combined ratio is 11.
The question asks us to work out the number of bungalows in the village. We are able to do this by multiplying the number of parts for bungalows in the combined ratio by what 1 part in the combined ratio represents. Bungalows has 8 parts in the combined ratio and 1 part in the combined ratio represents 11. The calculation for the number of bungalows in the village is:
The question asks us to work out the number of bungalows in the village. We are able to do this by multiplying the number of parts for bungalows in the combined ratio by what 1 part in the combined ratio represents. Bungalows has 8 parts in the combined ratio and 1 part in the combined ratio represents 11. The calculation for the number of bungalows in the village is:
This tells us that there are 88 bungalows in the village.
I have answered this question by combining the two separate ratios together to make one ratio, and I believe that this is the best method to answer this question. However, you could have found out the number of bungalows in the village by using the first ratio (flats to houses – 3 : 4) and there being 165 flats to find the number of houses. Then, you could have used the second ratio (houses to bungalows – 5 : 2) and the number of houses that you have just found to find the number of bungalows. Feel free to give this a go as you may find this method easier.
I have answered this question by combining the two separate ratios together to make one ratio, and I believe that this is the best method to answer this question. However, you could have found out the number of bungalows in the village by using the first ratio (flats to houses – 3 : 4) and there being 165 flats to find the number of houses. Then, you could have used the second ratio (houses to bungalows – 5 : 2) and the number of houses that you have just found to find the number of bungalows. Feel free to give this a go as you may find this method easier.