Back to OCR Circle Theorems (H) Home
4.8 A) Angles at the Centre & Circumference
4.8 A) Angles at the Centre & Circumference
There are seven circle theorems that we are going to look at throughout this whole section.
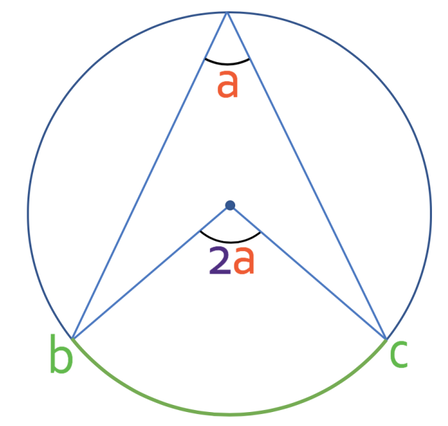
The first circle theorem is that the angle that is subtended by an arc at the centre of a circle is twice the angle subtended by the same arc at the circumference of the circle. Both of the angles on the diagram below are subtended by the same arc; they are both subtended by the arc between the points b and c (this arc has been coloured in green).
The first circle theorem is that the angle that is subtended by an arc at the centre of a circle is twice the angle subtended by the same arc at the circumference of the circle. Both of the angles on the diagram below are subtended by the same arc; they are both subtended by the arc between the points b and c (this arc has been coloured in green).
The angle at the centre is 2a and the angle that the circumference is a.
Example 1
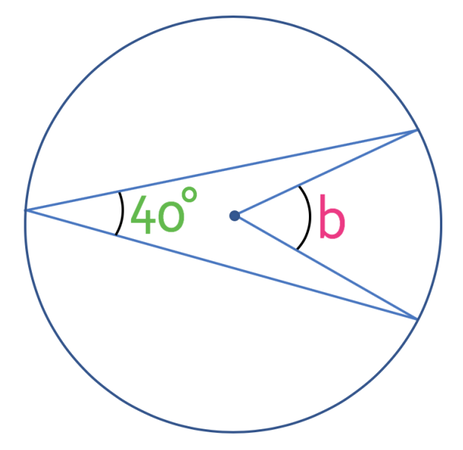
What is the size of angle b in the diagram below?
What is the size of angle b in the diagram below?
The angle that we are looking for and the angle that we are given are both subtended by the same arc. This means that the angle at the centre of the circle will be twice the size of the angle at the circumference of the circle. The angle at the circumference of the circle is 40° and we can find the angle at the centre of the circle by multiplying the angle at the circumference by 2. Therefore, the angle the centre of the circle is 80°.
Example 2
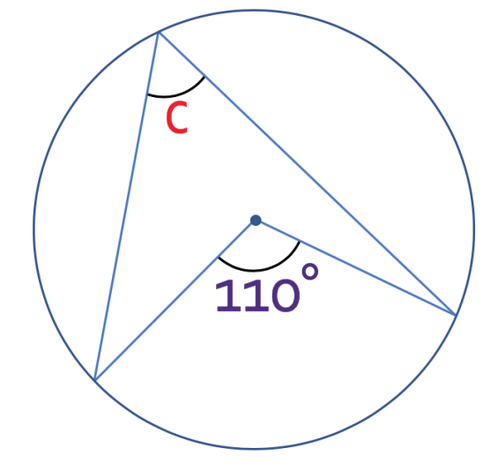
What is the size of angle c?
What is the size of angle c?
From the above diagram, we can see that the angle that we are given and the angle that we are trying to find are both subtended by the same arc. We know from the first circle theorem that the angle at the centre of a circle is twice the size of the angle at the circumference of a circle providing that both of the angels are subtended by the same arc (which they are). Another way to view this is that the angle at the circumference of the circle is half the size of the angle at the centre. Therefore, we find the size of c by dividing 110° by 2 and this gives us 55°.
Example 3
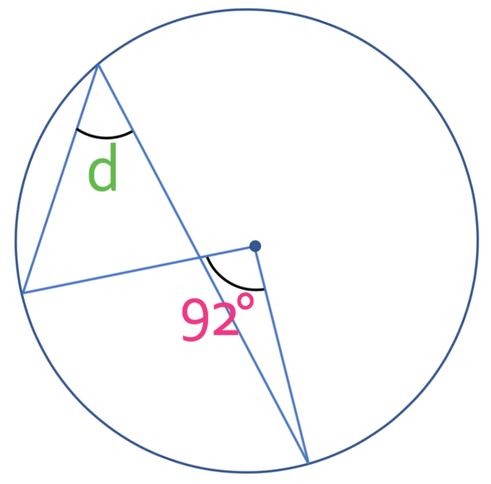
This circle theorem is very easy to spot when we have questions that look very similar to the circles above (when we have a shape that looks like a spaceship). However, sometimes it can be the case that the shape in the circle does not look as clean as the two examples that we have already looked at. The next example will be one whereby the shape makes it slightly harder to spot the circle theorem.
This circle theorem is very easy to spot when we have questions that look very similar to the circles above (when we have a shape that looks like a spaceship). However, sometimes it can be the case that the shape in the circle does not look as clean as the two examples that we have already looked at. The next example will be one whereby the shape makes it slightly harder to spot the circle theorem.
The angle that we are given and the angle that we want to find are both subtended by the same arc. This means that the angle at the centre of the circle will be twice the size of the angle at the circumference of the circle (or the angle at the circumference of the circle is half the size of the angle at the centre of the circle). The angle at the centre of the circle is 92° and we know that the angle at the circumference will be half the angle at the centre. Therefore, angle d is 46°.