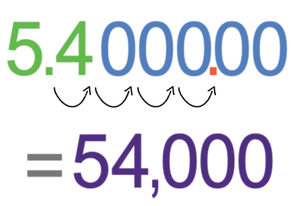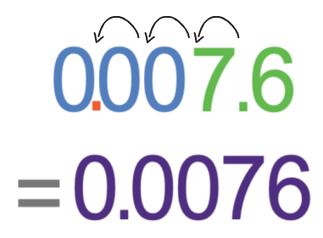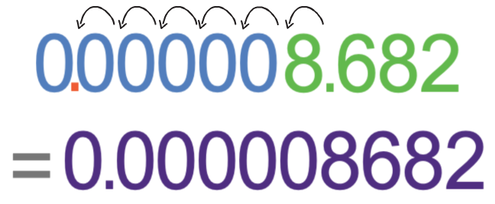Back to B1 Home
B1 B) Microscopy: Standard Form
B1 B) Microscopy: Standard Form
Throughout the whole of this science course, we will be working with very large and very small numbers. Sometimes it is easier to work with these numbers when they are in standard form. Standard form takes the following form:
Where:
When large numbers are written in standard form, they have a positive value for n. When small numbers are written in standard form, they have a negative value for n. Let’s look at large numbers first.
- A is a number between 1 and 10 (1 ≤ A < 10).
- n is the power of 10. It is the number of places that the decimal point moves.
When large numbers are written in standard form, they have a positive value for n. When small numbers are written in standard form, they have a negative value for n. Let’s look at large numbers first.
Large Numbers
Large numbers in standard form have a positive value for n.
Example 1
Write the number below out of standard form.
Large numbers in standard form have a positive value for n.
Example 1
Write the number below out of standard form.
The value of A is 5.4 and the value of n is 4. When the value of n is positive, we write out A with some 0’s on the right. We then move the decimal point n places to the right for a positive value of n; n is 4, so we move the decimal point 4 places to the right.
The number out of standard form is 54,000.
Example 2
Write the number below out of standard form.
Write the number below out of standard form.
The value of n is 5, which means that we will move the decimal point 5 places to the right. Therefore, we write the value of A down with some 0’s on the right, and move the decimal point 5 places to the right.
The number out of standard form is 724,000.
Placing Large Numbers into Standard Form
We are now going to place some large numbers into standard form. When we put numbers into standard form, we need to ensure that the value of A satisfies 1 ≤ A < 10.
Example 3
Write the number below in standard form.
We are now going to place some large numbers into standard form. When we put numbers into standard form, we need to ensure that the value of A satisfies 1 ≤ A < 10.
Example 3
Write the number below in standard form.
The first step is to find the value of A, which has to be between 1 and 10 (1 ≤ A < 10). For this number, the value of A is 6.7. We now count how many places the decimal point has moved when we change 67,000 to 6.7.
We can see that the decimal point has moved by 4 places, thus meaning that n is 4. Therefore, 67,000 written in standard form is:
Example 4
Write the number below in standard form.
Write the number below in standard form.
The value of A for this number is 3.5. We now see how many places the decimal point has moved when we go from 3,500,000 to 3.5.
We can see that the decimal point has moved by 6 places, thus meaning that the value for n is 6. Therefore, 3,500,000 written in standard form is:
Small Numbers
Small numbers in standard form have a negative value for n.
Example 1
Take the number below out of standard form.
Small numbers in standard form have a negative value for n.
Example 1
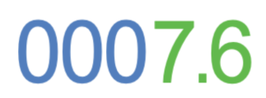
Take the number below out of standard form.
The value of n is negative (n is -3), which means that this will be a small number. For small numbers, we write out A with some 0’s to the left of A.
The value of n is -3, which means that we move the decimal point 3 places to the left.
The number out of standard form is 0.0076
Example 2
Take the number below out of standard form.
Take the number below out of standard form.
The value of n is negative (-6), so we write down A with some 0’s to the left of A. We then move the decimal point 6 places to the left because n is -6.
The number out of standard form is 0.000008682
Placing Small Numbers Into Standard Form
We are now going to place some small numbers into standard form. When we put numbers into standard form, we need to ensure that the value of A satisfies 1 ≤ A < 10.
Example 3
Place the number below into standard form.
We are now going to place some small numbers into standard form. When we put numbers into standard form, we need to ensure that the value of A satisfies 1 ≤ A < 10.
Example 3
Place the number below into standard form.
The first step is to choose our value of A, which needs to satisfy 1 ≤ A < 10. The value of A for 0.004 would be 4. The next step is to see how many places we have to move the decimal point in order to give us 4.
From the diagram above, we can see that we move the decimal point 3 places to the right. Therefore, n is -3. So, 0.004 in standard form is:
Example 4
Place the number below into standard form.
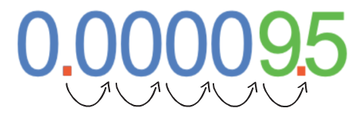
Place the number below into standard form.
Our value for A will be 9.5. We now need to find out how many places we move the decimal point.
From the diagram above, we can see that we move the decimal point 5 places to the right, thus meaning that n is -5. Therefore, 0.000095 written in standard form is:
Final Points
The form for standard form is:
The form for standard form is:
The value for A must always satisfy 1 ≤ A < 10. Large numbers have positive values for n. Small numbers have negative values for n.