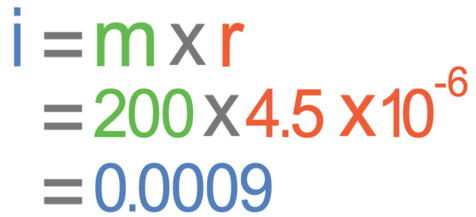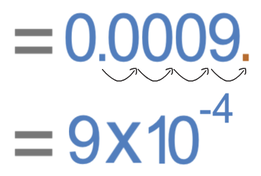B1 D) Microscopy: Magnification Calculations
There are two microscopes that you need to know about. These are light microscopes and electron microscopes.
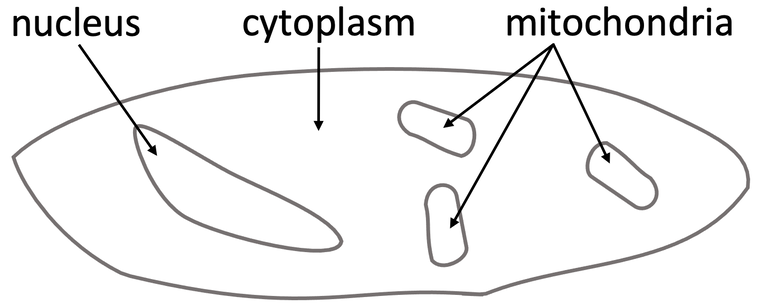
- Light microscopes were invented in the 1590s, and they pass light through a specimen. They allowed scientists to see large subcellular structures in cells, such as nuclei and chloroplasts.
- Electron microscopes were invented in the 1930s, and they use electrons (hence the name). They have a higher magnification and resolution than light microscopes. This allowed scientists to see cells closer up and in greater detail. When we look at cells through an electron microscope we can see ribosomes, mitochondria and the formation of the nucleus in more detail.
Magnification refers to how many times bigger the object is when looking through a microscope compared to real life. We can find the magnification of a microscope by dividing the image size by the real size.
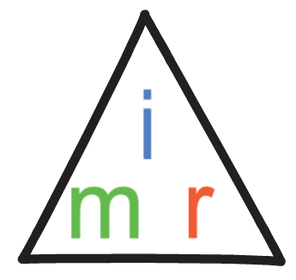
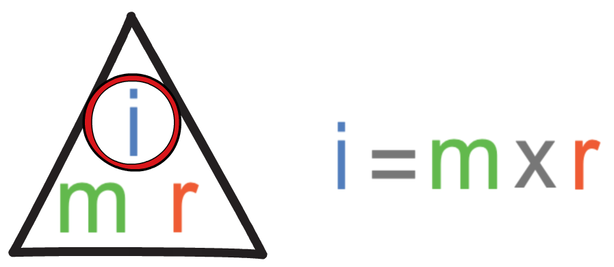
The formula triangle for magnification (m), image size (i) and real size (r) is shown below.
I look at a bacteria cell through a microscope that has a magnification of x100. The length of the bacteria cell in the image produced by the microscope is 4 mm. Find the real length of the bacteria cell. Give your answer in micrometres (μm).
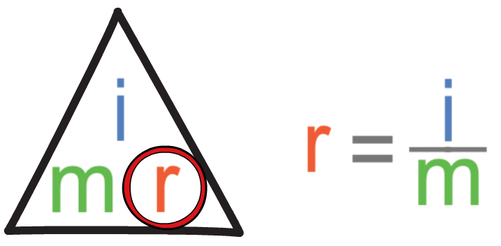
The question is asking us to find the real length of the bacteria. We find the calculation that we need to undertake by covering up the real size (r) in the formula triangle. When we do this, we see that we find the real size by dividing the image size by the magnification.
The question asked us to give our answer in micrometres (μm). 1 mm is 1000 μm, so we convert millimetres (mm) to micrometres (μm) by multiplying by 1000.
Sometimes we will be given a scale drawing of a specimen from a microscope and the real size of the specimen. We will then be asked to find the magnification of the microscope. We find the magnification by measuring the length of the specimen on the scale drawing (the image size). We then sub the values into the calculation from the formula triangle to find the magnification. Let’s have an example.
Question
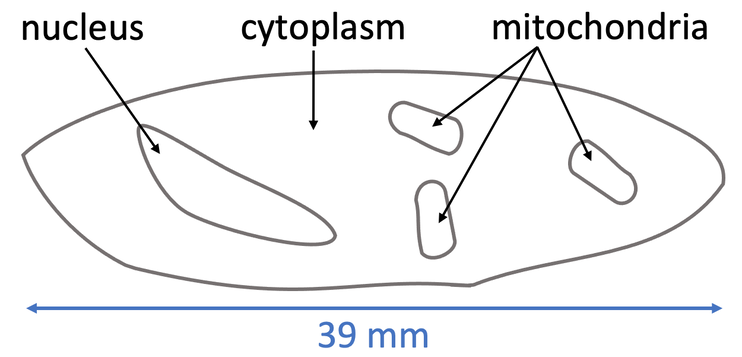
A student looked through a microscope and completed a scale drawing, which is shown below.
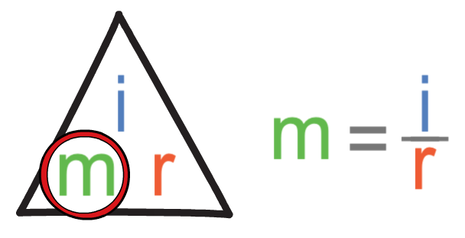
The question is asking us to find the magnification (m). When we cover magnification up in the formula triangle, we see that we find the magnification by dividing the image size by the real size.
We are now going to have a look at an example where the values are in standard form. We answer these questions in exactly the same way; we just need to be careful when we sub the values into the calculation (especially when we are dividing).
Question
A specimen has a width of 4.5 x 10-6 m. The specimen is viewed through a microscope with a magnification of 200. Find the width of the image under the microscope. Give your answer in metres and in standard form.
The question is asking us to find the image size (i). When we cover image size up in the formula triangle, we see that we find the image size by multiplying the magnification by the real size.
The question tells us that the magnification is 200 and the real size is 4.5 x 10-6; we sub these values into the calculation.
The image size is 0.0009 metres. We now need to put this value into standard form. The value of A in standard form must be between 1 and 10 (1 ≤ A < 10). The value of A for 0.0009 would be 9.
The next step is to see how many places we move the decimal point in order to give us 9.
From the diagram above, we can see that we move the decimal point 4 places to the right. Therefore, n is -4. So, 0.0009 in standard form is 9 x 10-4.
The image size is 9 x 10-4 metres.