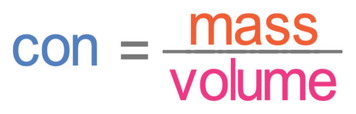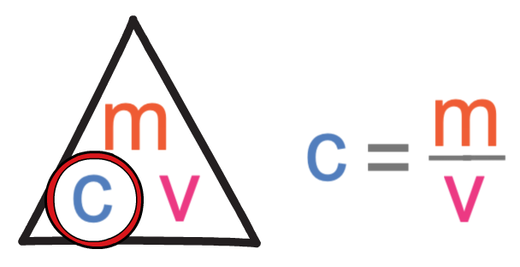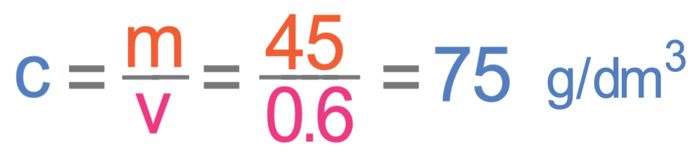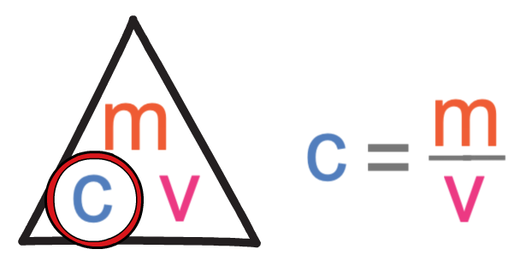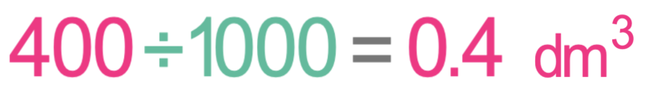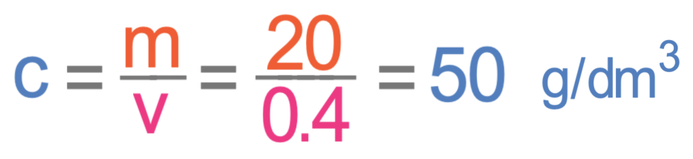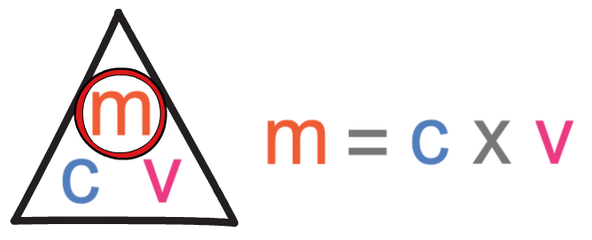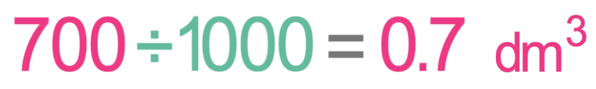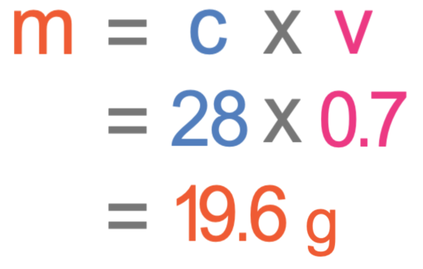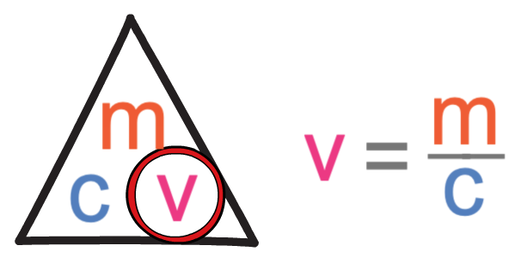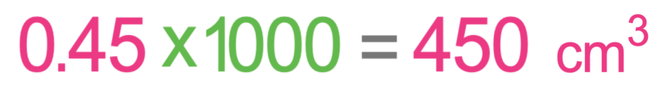Back to C3 Home
​C3 G) Concentrations of Solutions
Concentration measures how much of a solute we have in a given volume. A solute is a substance that can be dissolved to make a solution. A greater concentration means that we have more of a solute in a given volume. A lower concentration means that we have less of a solute in a given volume. We work out the concentration of a solution by dividing the mass of the solute by the volume of the solution.

Mass is measured in grams and volume is measured in dm3 (1 dm3 is 1,000 cm3). This means that concentration is measured in g/dm3.

 

The formula triangle for concentration is shown below:

​Concentration is dependent upon the mass of the solute (m) and the volume that you are dissolving the solute in (v). If you increase the mass of the solute and keep the volume the same, the concentration will increase (and vice versa). If you increase the volume and keep the mass of the solute the same, the concentration will decrease (and vice versa).
 
Let’s now have a few examples.
Example 1

What is the concentration of a copper chloride solution if 45 g of copper chloride is dissolved in 0.6 dm3 of water?

 

The question is asking us to work out concentration, which we are able to do by dividing the mass by the volume.

For the above equation, the mass should be measured in grams and the volume should be measured in dm3. The question tells us that the mass is 45 grams and the volume is 0.6 dm3. Both of these values are in the correct units, which means that we just sub the values into their appropriate places in the calculation; we sub the mass in as 45 g and the volume in as 0.6 dm3.

The concentration is 75 g/dm3.

Example 2

The previous example was fairly straightforward as both of the values were in the correct units. We are now going to have a look at an example whereby the values are not in the correct units.

 

What is the concentration in g/dm3 of 20 g of sodium chloride in 400 cm3 of water?

 

We are asked to work out the concentration of the solution, which means that we divide the mass by the volume.

For the above equation, the mass should be measured in grams and the volume should be measured in dm3. The question tells us that the mass is 20 grams and the volume is 400 cm3. The mass is currently in the correct units, but the volume is not; the volume is currently in cm3 and not dm3. 1 dm3 is 1000 cm3. Therefore, we convert from cm3 to dm3 by dividing by 1000.

This means that the volume of water in dm3 is 0.4 dm3.

 

We now have both the mass and volume in the correct units, which means that we can sub the mass in as 20 g and the volume in as 0.4 dm3.

The concentration is 50 g/dm3.

Example 3

What mass of a salt would you need to dissolve in 700 cm3 of water to make a solution with a concentration of 28 g/dm3?

 

The question is asking us to work out the mass. We find the calculation for mass by covering up mass in the formula triangle. When we cover up mass, it tells us that we work out the mass by multiplying the concentration by the volume.

For the above calculation, the concentration needs to be in g/dm3 and the volume needs to be in dm3. We were told in the question that the concentration is 28 g/dm3 and the volume is 700 cm3. The concentration is in the correct units, but the volume is not; we need to convert the volume from cm3 to dm3. We are able to convert cm3 to dm3 by dividing by 1000.

We now have the concentration and volume in the correct units; the concentration is 28 g/dm3 and the volume is 0.7 dm3. We sub these values into the calculation to find the mass.

The mass needed is 19.6 grams.

Example 4

I am going to dissolve 63 grams of a salt in some water. What volume of water should I dissolve the 63 grams of salt in if I want to create a solution with a concentration of 140 g/dm3? Give your answer in cm3.

 

The first step in answering this question is to find out the calculation that we need to undertake to find the volume, which we are able to do by covering up volume in the formula triangle. When we cover up volume, we see that we find the volume by dividing the mass by concentration.

For the above calculation, the mass will be in grams and the concentration will be in g/dm3. The question tells us that the mass is 63 grams and the concentration is 140 g/dm3. Both of these values are in the correct units. Therefore, we sub in the mass as 63 and the concentration as 140.

The volume of water that we need to dissolve our salt in is 0.45 dm3. The question asks us to give our volume in cm3 and not dm3. 1 dm3 is 1000 cm3. Therefore, we are able to convert dm3 to cm3 by multiplying by 1000.

The volume of water that we dissolved the 63 grams of salt in is 450 cm3.