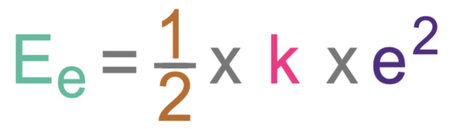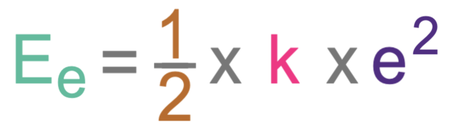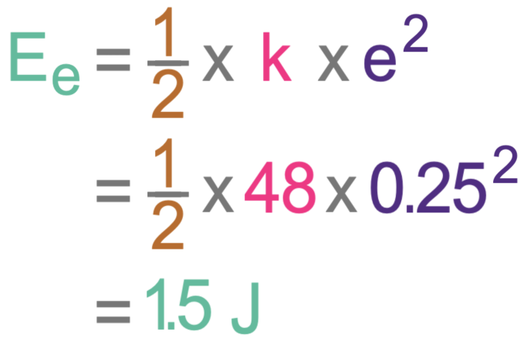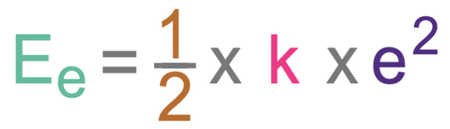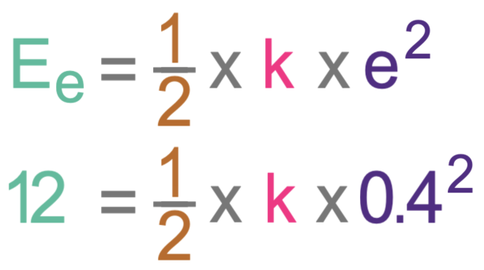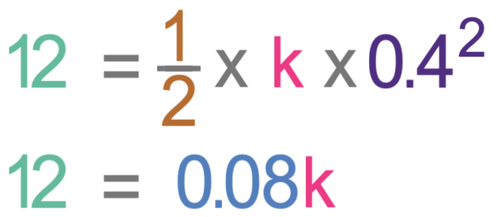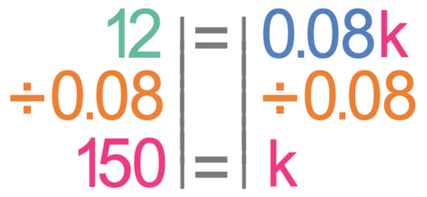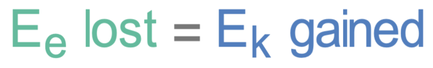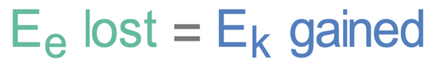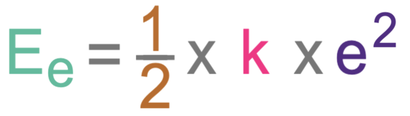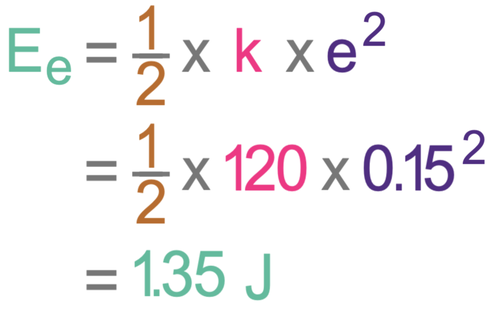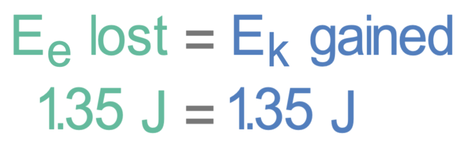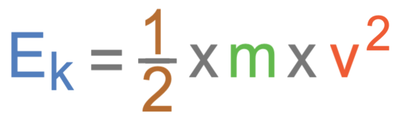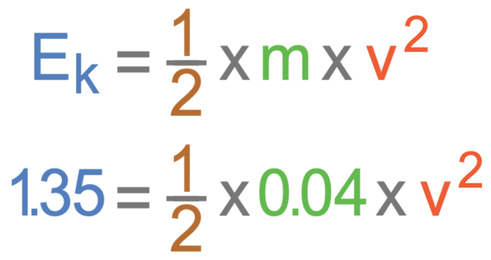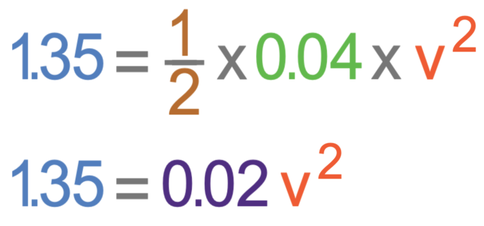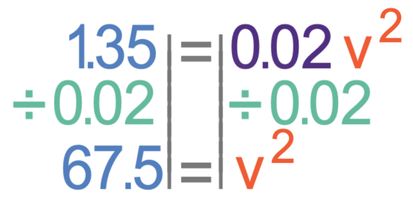Back to P1 Home
​P1 C) Elastic Potential Energy
When a force is applied to an elastic object, the object will stretch/ change shape and store energy in its elastic potential energy store. When the force is removed, energy from the object’s elastic potential energy store is transferred to the object’s kinetic energy store and the object reverts back to its original shape.
 
We can work out the amount of energy in an elastic object’s elastic potential energy store by using the formula below:

In the formula, Ee is elastic potential energy measured in joules (J), k is the spring constant in newtons per metre (N/m) and e is the extension in metres (m).

 

k in the above formula is the spring constant, which tells us the force that we have to put in to extend a spring. All springs are different and therefore have different spring constants (different values for k). For example, a spring in a clickable pen will have quite a low spring constant, and a spring in a mattress will have a greater spring constant.

 

e in the above formula is extension, which can be viewed as change in shape. Springs can be stretched and compressed. We sub the value for both stretching and compression as positive values into the elastic potential energy formula.

 

The working for finding the amount of energy in a spring’s elastic potential energy store is very similar to the working for finding the amount of energy in a moving object’s kinetic energy store.

Example 1

Rea stretches a spring 0.25 metres. The spring has a spring constant of 48 N/m. Find the amount of energy in the spring’s elastic potential energy store.

 

We find the amount of energy in the spring’s elastic potential energy store (Ee) by using the formula below.

​k in the above formula is the spring constant, which is 48 N/m. e is the extension of the spring which is 0.25 metres. Both of these values are in the correct units, so we sub k in as 48 and e in as 0.25 into the formula.
​The amount of energy in the spring’s elastic potential energy stores is 1.5 joules.
Example 2
Two carts that are connected by a spring hit a wall and compress by 40 cm. The amount of energy in the spring’s elastic potential energy store is 12 joules. Find the spring constant for the spring.
 
We find the spring constant (k) by using the formula below.

The question tells us that the amount of energy in the spring’s elastic potential energy store is 12 joules. We are also told that the spring compresses by 40 cm. Extension or compression is measured in metres, which means that we need to convert 40 centimetres to metres, which we can do by dividing by 100; the compression is 0.4 metres (40 ÷ 100 = 0.4). We sub these values into the elastic potential energy formula; we sub Ee as 12 and e as 0.4.

We then solve in the same way that we would solve an algebraic maths equation. The first step in solving this equation is to multiply the ½ and the 0.42 on the right side of the equation.

​We want to find the value of k and not 0.08 k. Therefore, we divide both sides of the equation by 0.08.
This means that the spring constant for this spring is 150 N/m.
Energy Being Transferred
We are now going to have a look at an example whereby a spring is used to fire a ball. In order for the spring to fire a ball, the spring will be compressed, which causes energy to be stored in the spring’s elastic potential energy store. When the spring is released, the spring will return to its original shape and energy will be transferred from the spring’s elastic potential energy store to the kinetic energy store of the ball, which results in the ball being fired. The amount of energy that is lost from the spring’s elastic potential energy store will be equal to the amount of energy gained in the ball’s kinetic energy store. This gives us the equation below.
This equation is based on the assumption that all of the energy from the spring’s elastic potential energy store is fully transferred to the ball’s kinetic energy store. However, in reality, some of the energy from the spring’s elastic potential energy store will be transferred to other energy stores, such as the thermal energy stores of the spring, the ball and the air.
 
Let’s now have an example.
 
Example 3
A student uses a spring to fire a ball that has a mass of 40 grams into the air. The spring has a spring constant of 120 N/m and the student compresses the spring by 0.15 metres. Calculate the velocity of the ball immediately after it is fired by the spring. Give your answer to 2 significant figures and assume that all of the energy from the spring is transferred to the ball.
 
The compression of the spring results in energy being stored in the spring’s elastic potential energy store. When the spring is let go, the spring will return to its original shape and transfer all of the energy that was in its elastic potential energy store to the kinetic energy store of the ball. This means that the elastic potential energy lost from the spring will be equal to the kinetic energy gained by the ball. This gives us the equation below.
We can work out the elastic potential energy lost by using the elastic potential energy formula, which is shown below.
The question tells us that the spring constant is 120 N/m and the spring is compressed by 0.15 metres. Both of these values are in the correct units, so we can sub them into the formula; we sub in k as 120 and e as 0.15.
Therefore, the energy lost in the spring’s elastic potential energy store is 1.35 joules. All of the energy lost from the spring’s elastic potential energy store will be transferred to the kinetic energy store of the ball.
This means that the energy in the ball’s kinetic energy store will be 1.35 joules. The formula for kinetic energy is shown below.
​We are looking for the velocity of the ball, which is the value of v. We have found that the kinetic energy of the ball is 1.35 joules. The question told us that the mass of the ball is 40 grams. Mass in this formula needs to be in kilograms, so we need to convert the mass from grams to kilograms, which we do by dividing by 1,000; the mass is 0.04 kg (40 ÷ 1,000 = 0.04). We sub the kinetic energy as 1.35 and the mass as 0.04 into the formula.
We then solve like a maths equation to find the value of v. The first step in solving is to multiply all of the stuff on the right side of the equation.

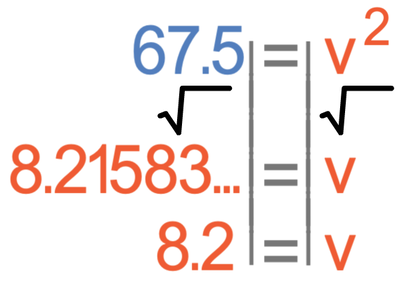
The next step is to find the value of v2, which we do by dividing both sides of the equation by 0.02.

We want to find the value of v and not v2. Therefore, we square root both sides of the equation.

Therefore, the velocity of the ball immediately after it is fired is 8.2 m/s (to 2 significant figures).