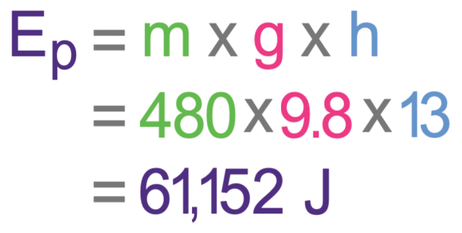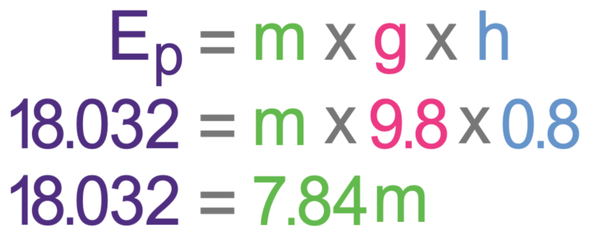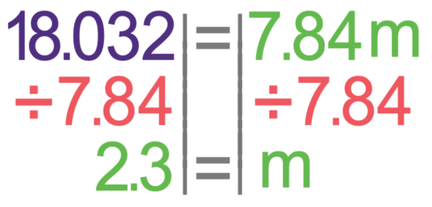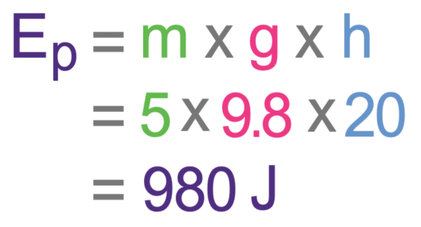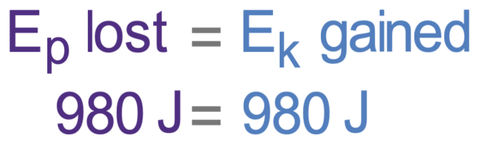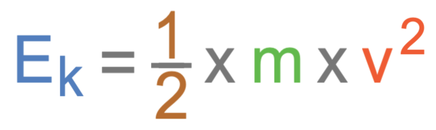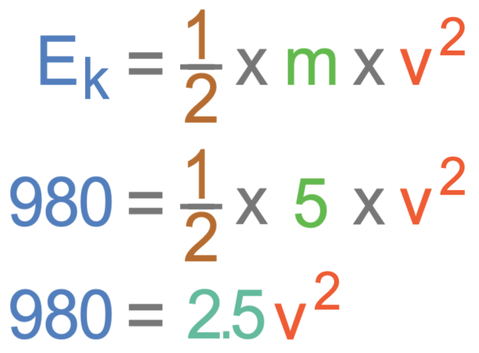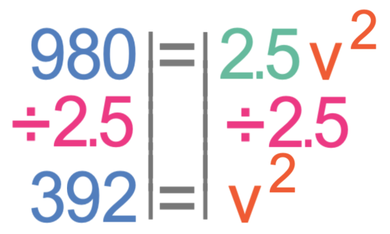P1 D) Gravitational Potential Energy
Also, if we had 2 objects with different masses at the same height, the object with the larger mass will have more energy in its gravitational potential energy store. For example, if we had a laptop and a pen on a desk, the laptop would have more energy in its gravitational potential energy store because it has a greater mass.
The formula for change in gravitational potential energy is:
Where Ep is change in gravitational potential energy measured in joules (J), m is the mass measured in kilograms (kg), g is the gravitational field strength measured in newtons per kilogram (N/kg) and h is the change in height in metres (m).
Let’s now have a few examples of using the gravitational potential energy formula.
A piano on earth is lifted up to the third floor of a building. The piano has a mass of 480 kg and the third floor is 13 metres above the ground floor where the piano currently sits. Work out the change in energy in the piano’s gravitational potential energy store.
Use g as 9.8 N/kg.
The question is asking us to work out the change in gravitational potential energy (Ep), which we are able to do by using the formula below.
We are told in the question that the mass (m) of the piano is 480 kg, the gravitational field strength (g) is 9.8 N/kg and the change in height (h) is 13 m. All of these are in the correct units, so we can sub them into the formula to find Ep.
A laptop is lifted from the floor to a table that is 80 cm above the floor. The change in energy in the laptop’s gravitational potential energy store is 18.032 joules. Find the mass of the laptop.
Use g as 9.8 N/kg.
Like the question before, we answer this question by using the gravitational potential energy formula, which is shown below.
We are looking for the mass which is m in the above formula. We find the mass by subbing in the values that we are given in the question. The question tells us that the change in gravitational potential energy for the laptop is 18.032 joules. Also, we are told that the change in height is 80 cm. The change in height in the formula needs to be in metres. There are 100 cm in 1 metre, so we can convert cm to metres by dividing by 100; the change in height in metres is 0.8 m (80 ÷ 100 = 0.8). We are also told that g is 9.8 N/kg. We sub Ep as 18.032, g as 9.8 and h as 0.8 into the formula.
When an object falls, energy is transferred from the object’s gravitational potential energy stores to the object’s kinetic energy stores (the object starts moving). If we assume that there is no air resistance, all of the energy that is lost from the object’s gravitational potential energy store is transferred to the object’s kinetic energy store. This gives us the equation below:
We assumed that there was no air resistance acting on the object when the object fell, and this meant that all of the energy that was lost from the object’s gravitational potential energy store was transferred to the object’s kinetic energy store. However, in reality, there will be air resistance and some of the energy from the object’s gravitational potential energy store will be transferred to other energy stores, such as the thermal energy stores of both the object and the surroundings.
Example 3
A 5 kg object is stationary. It then falls from a height of 20 metres. Find the speed of the object after it has fallen 20 metres. Give your answer to 3 significant figures.
Use g as 9.8 N/kg and assume that there is no air resistance.
The question tells us that the object is falling. When the object falls, energy is transferred from the object’s gravitational potential energy store to the object’s kinetic energy store. The question tells us that there is no air resistance. This means that all of the energy that is lost from the object’s gravitational potential energy store will be transferred to the object’s kinetic energy store. This gives us the equation below.
The first step in answering this question is to work out the amount of energy that was lost from the object’s gravitational potential energy store (Ep). We are able to do this by using the formula below.
The question tells us that the mass of the object is 5 kg, gravity is 9.8 N/kg and the change in height is 20 m. We sub m as 5, g as 9.8 and h as 20 into the formula to find the amount of energy that has been lost from the object’s gravitational potential energy store.
This tells us that the amount of energy lost in the object’s gravitational potential energy store is 980 joules. As we have assumed that there is no air resistance, all of the energy that is lost from the object’s gravitational potential energy store will be transferred to the object’s kinetic energy store.
This means that the energy in the object’s kinetic energy store will be 980 joules. The formula for kinetic energy is shown below.
We are looking for the speed of the object, which is the value of v. We have found that the kinetic energy is 980 joules, and we are told in the question that the mass of the object is 5 kg; we sub these values into the kinetic energy formula.
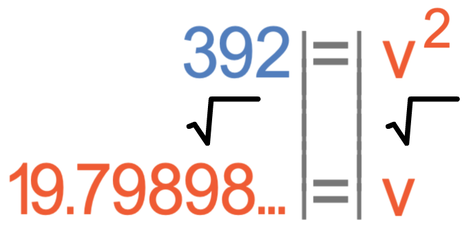
We now solve the equation to find the value of v. The first step in finding the value of v is to divide both sides of the equation by 2.5.
We want to find the value of v and not v2. Therefore, we square root both sides of the equation.
We are asked in the question to give our speed to 3 significant figures.
Therefore, the speed of the object is 19.8 m/s.