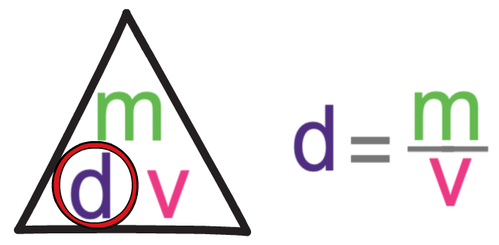Back to P3 Home
P3 D) Density – Part 2

We can work out the density of a substance by dividing its mass by its volume. The formula triangle and calculation for density are shown below:

The density of a substance depends on two factors.
 
Factor 1
One of the factors is what the substance is made out of. Certain substances have a greater density than other substances. For example, gold is denser than polystyrene.
 
Factor 2
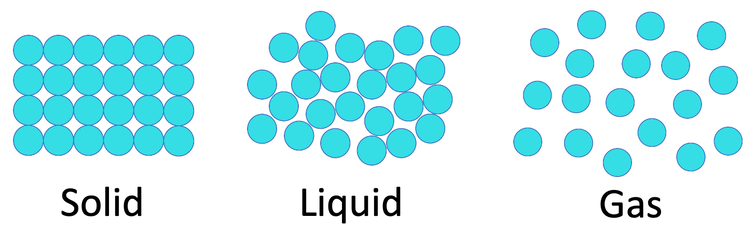
The second factor is the arrangement of the particles. The closer together the particles are for a given substance, the greater the mass is for a given volume, which results in a greater density. On the first webpage of this whole subsection, we looked at the arrangement of the particles in a solid, liquid and gas. The arrangement of the particles in the 3 different states are shown below.

From looking at the 3 states of matter, we can see that the particles are the closest together in solids, then liquids and the furthest away in gases. This means that solids will have the greatest density, then liquids and gases will have the lowest density. Solids have the greatest density because the particles are the closest together in solids. The densities for solids and liquids will be fairly similar because the arrangement/ closeness of the particles is fairly similar. The density of gases will be considerably less than the densities of liquids and solids.

---

Working Out Volume & Mass
We work out the density of a substance by dividing the mass by the volume. The process for working out the density of a solid and a liquid is shown below.
 
Solids
We can find the mass of a solid by placing the solid on a mass balance (a set of scales). We can change the settings on the mass balance to give us the mass in g or kg.
 
We then need to find the volume of the object. If the object is a regular shape, we find the volume of the object by using the standard formulas. For example, if the object was a cuboid, we find the volume by multiplying the length by the width by the height. If the object was a prism, we find the volume by multiplying the area of the cross section by the length of the prism.
 
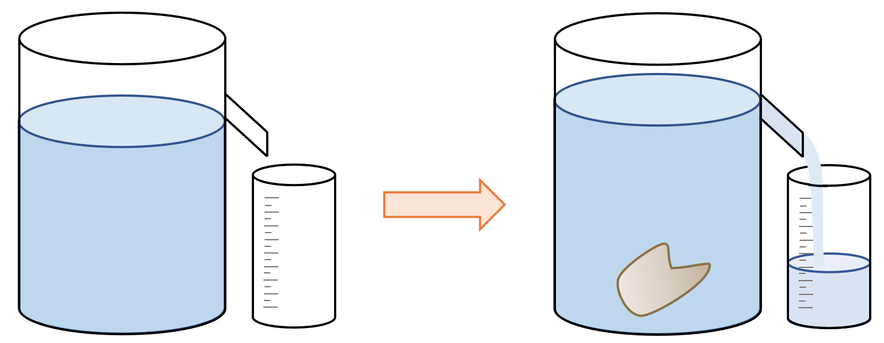
However, if the object is an irregular shape, we can use a eureka can to find the volume. A diagram of a eureka can is shown below.

We use a eureka can by filling it up with water to the spout. We then place an empty beaker underneath the spout. We then gently lower the object that we are finding the volume of into the water; we can lower the object into the water by tying the object to a piece of string. As the object enters the water, it will displace some water, which will go down the spout and into the beaker. When the spout has stopped dripping, we measure the volume of water in the beaker. The volume of water in the beaker will be the same as the volume of the object because the object has displaced this volume of water causing it to run down the spout and into the beaker. 1 ml is 1 cm³, so if the quantity of water in the beaker was 36 ml, the object would have a volume of 36 cm³.

 

We need to ensure that we gently place the object into the water rather than dropping the object into the water. This is because waves will be created if we drop the object into the water and these waves will result in more water passing down the spout and into the beaker, thus meaning that we would get an incorrect value for the volume of the object (our value for volume would be too large).

 

We now have all of the values that we need to work out density; we have the mass (from the mass balance) and the volume (from a calculation for a regular shape or the eureka can for an irregular object). We work out density by dividing the mass by the volume.

 
Liquids

We measure the mass of a liquid by placing an empty beaker onto a mass balance and pressing 0 to make this mass 0. We then pour in a certain volume of the liquid (like 50 ml) into the beaker on the mass balance and measure the mass. We now have the mass of the liquid (measured from the mass balance) and the volume of the liquid (for my example 50 ml, which is 50 cm³; 1 ml = 1 cm³), which means that we can work out the density of the liquid; we work out the density of the liquid by dividing the mass by the volume.