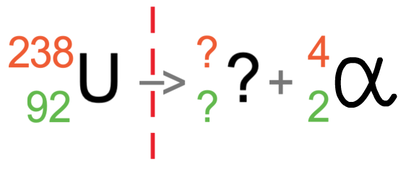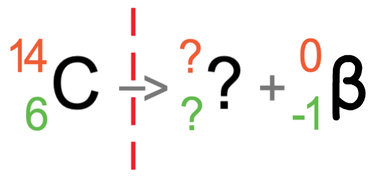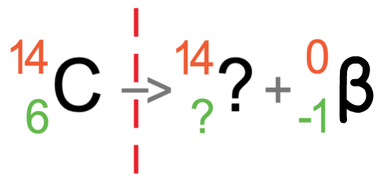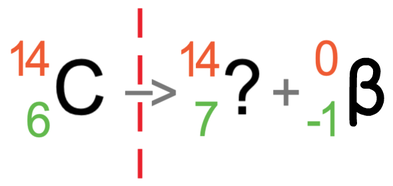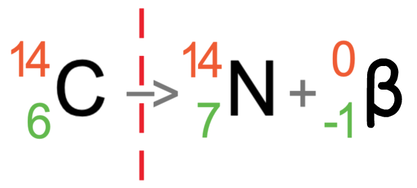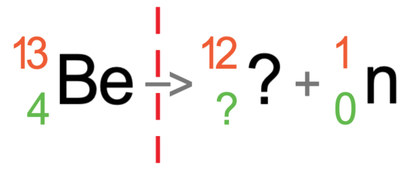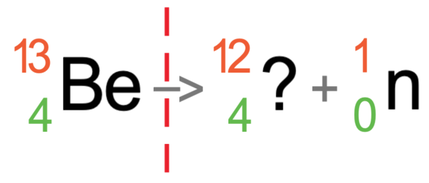We are going to be looking at nuclear equations in this section. When we work with nuclear equations, we need to remember that the numbers before and after the radiation has taken place need to be equal; the total mass numbers (top numbers) and total atomic numbers (bottom numbers) need to equal one another on either side of the arrow. All of the nuclear equations will take the following form:
Sometimes it may be the case that there is more than one type of radiation that is given off, such as alpha radiation and gamma radiation. If this is the case, we just add the additional radiation to the end. The rules for working out the missing numbers will be the same; the total mass numbers (top numbers) and total atomic numbers (bottom numbers) need to equal one another on either side of the arrow.
Alpha
Let’s suppose that we have uranium and it is going to emit alpha radiation. Uranium has a mass number of 238 and an atomic number of 92. The tile for uranium is shown below with the partially filled equation:
Let’s suppose that we have uranium and it is going to emit alpha radiation. Uranium has a mass number of 238 and an atomic number of 92. The tile for uranium is shown below with the partially filled equation:
An alpha particle has 2 protons and 2 neutrons (it is a helium nuclei). This means that it has an atomic number of 2 and a mass number of 4. I have added the symbol and numbers for alpha radiation to the equation.
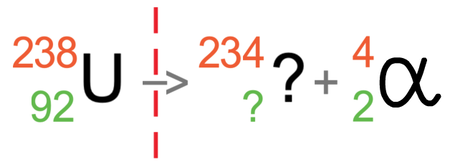
We now need to find the values for the atomic number and mass number for the atom after the radiation has taken place. The rule is that the numbers must equal each other on either side of the reaction arrow.
Let’s work it out for the mass number first (the top number). The mass number on the left is 238, and this must be equal to the sum of the mass numbers on the right. On the right, we do not know the mass number for the atom after the radiation has taken place (I will call this number the unknown), but we do know that alpha radiation has a mass number of 4; this means that 4 plus the unknown will equal 238. We can find the value of this unknown by taking 4 from 238, which tells us that the mass number for the atom after the radiation has taken place is 234 (238 – 4 = 234).
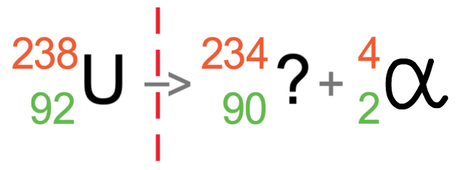
We now do the same for the atomic number (the bottom number). The atomic number on the left is 92, which must be equal to the sum of the atomic numbers on the right. On the right, we do not know the atomic number for the atom after the radiation has taken place (I will call this the unknown), but we do know that alpha radiation has an atomic number of 2; this means 2 plus the unknown will equal 92. We can find the value of this unknown by taking 2 from 92, which tells us that the atomic number for the atom after the radiation has taken place is 90 (92 – 2 = 90).
After the alpha particle has been fired out, we will have a different element because the number of protons in our atom has decreased by 2; uranium had 92 protons and the atom after the radiation has taken place has 90 protons. The element that has 90 protons is thorium, which has the symbol Th. We can replace the ? mark with Th.
I am now going to put the number of protons and neutrons underneath uranium, thorium and the alpha particle; the number of protons is the atomic number (bottom number) and the number of neutrons is the mass number minus the atomic number (top number – bottom number).
We know that an alpha particle is 2 protons and 2 neutrons, so after the alpha particle has been emitted, the number of protons should go down by 2 and the number of neutrons should also go down by 2. We can see that this is the case by looking at the number of protons and neutrons; before the radiation took place, the atom had 92 protons and now it has 90 protons (2 less), and before the radiation took place, the atom had 146 neutrons and now it has 144 neutrons (2 less).
Beta
Let’s now have an example of carbon-14 emitting beta radiation. Carbon-14 has an atomic number of 6 and a mass number of 14. This means that it has 6 protons and 8 neutrons (14 – 6). The tile for carbon-14 is shown below with the partially filled equation:
Let’s now have an example of carbon-14 emitting beta radiation. Carbon-14 has an atomic number of 6 and a mass number of 14. This means that it has 6 protons and 8 neutrons (14 – 6). The tile for carbon-14 is shown below with the partially filled equation:
Beta radiation is where a neutron turns into a proton and an electron. The proton is kept in the nucleus and the electron is fired out. As beta radiation is an electron and electrons are negatively charged, a beta particle will have an atomic number of -1 and a mass number of 0 (electrons have essentially no mass). I have added the symbol for beta radiation to the equation.
We now need to find the values for the atomic number and mass number for the atom after the radiation has taken place. The rule is that the numbers must equal each other on either side of the reaction arrow.
Let’s work it out for the mass number first (the top number). The mass number on the left is 14, and this must be equal to the sum of the mass numbers on the right. On the right, we do not know the mass number for the atom after the radiation has taken place (I will call this the unknown), but we do know that beta radiation has a mass number of 0. This means that the mass number for the atom after the radiation has taken place will be the same as it was before the radiation took place; it will be 14.
We now do the same for the atomic numbers (the bottom numbers). The atomic number on the left is 6, which must be equal to the sum of the atomic numbers on the right. On the right, we do not know the atomic number for the atom after the radiation has taken place (I will call this the unknown), but we do know that beta radiation has an atomic number of -1. As the numbers for the atomic numbers will equal, it means that -1 plus the unknown will equal 6. We can find the value of this unknown by taking -1 from 6, which tells us that the atomic number for the atom after the radiation has taken place is 7 (6 – -1 = 6 + 1 = 7).
It is the number of protons (the atomic number) that determines what element an atom is. The atom after the nuclear decay has taken place has 7 protons. We can use the periodic table to find which element has 7 protons, and when we do this, we see that the element that has 7 protons is nitrogen; the atom after the radiation has taken place is nitrogen (N).
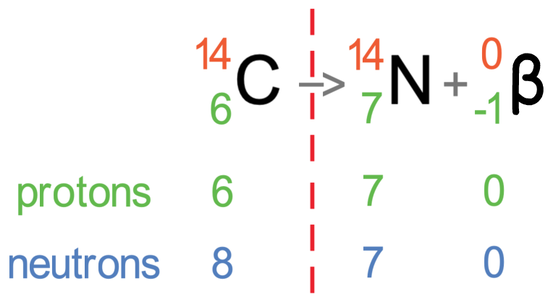
I am now going to put the number of protons and neutrons underneath carbon, nitrogen and the beta particle; the number of protons is the atomic number (bottom number) and the number of neutrons is the mass number minus the atomic number (top number – bottom number).
Carbon-14 contained 6 protons and 8 neutrons. During beta radiation, a neutron in carbon-14 turned into a proton and an electron (beta). As a neutron was used in the beta radiation, the number of neutrons decreases by 1; this is what happened because carbon-14 had 8 neutrons and nitrogen has 7 neutrons (1 less). The neutron was turned into a proton and the proton was kept in the nuclei, which means that the number of protons increases by 1; this is what happened because carbon-14 had 6 protons and nitrogen has 7 protons (1 more). The neutron also turned into an electron that was fired out of the nuclei, so this electron has no effect on the number of protons and neutrons.
Neutron
We are now going to have a look at beryllium-13 emitting neutron radiation. Beryllium-13 has an atomic number of 4 and a mass number of 13. This means that it has 4 protons and 9 neutrons (13 – 4). The tile for beryllium-13 is shown below with the partially filled equation:
We are now going to have a look at beryllium-13 emitting neutron radiation. Beryllium-13 has an atomic number of 4 and a mass number of 13. This means that it has 4 protons and 9 neutrons (13 – 4). The tile for beryllium-13 is shown below with the partially filled equation:
Neutron radiation is where the nucleus of an atom fires out a neutron. A neutron has a neutral charge and a mass of 1. This means that the atomic number for neutron radiation is 0 and the mass number is 1. I have added the symbol for neutron radiation to the equation.
We now need to find the values for the atomic number and mass number for the atom after the radiation has taken place. The rule is that the numbers must equal each other on either side of the reaction arrow.
Neutron radiation has a mass number of 1, and this means that the mass number for the atom after the radiation has taken place will be 1 less than the mass number for the atom before the radiation has taken place. This means that the mass number becomes 12 (13 – 1 = 12).
Neutron radiation has a mass number of 1, and this means that the mass number for the atom after the radiation has taken place will be 1 less than the mass number for the atom before the radiation has taken place. This means that the mass number becomes 12 (13 – 1 = 12).
Neutron radiation has an atomic number of 0. This means that the atomic number for the atom before and after the radiation has taken place will be the same; the mass number for the atom after the radiation has taken place will be 4.
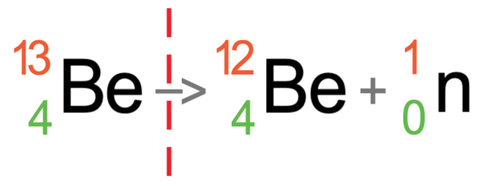
The atom before and after the radiation has taken place has the same number of protons. This means that the atom after the radiation has taken place will remain as beryllium (remember, it is the number of protons that determines what element an atom is).
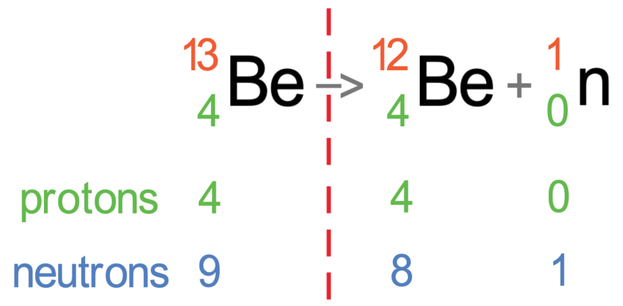
I am now going to work out the number of protons and neutrons in the atom before and after the radiation has taken place.
Before the radiation has taken place, beryllium had 4 protons and 9 neutrons. It then fires out 1 neutron, which means that the number of neutrons will decrease by 1; this is what happened because the atom before the radiation took place had 9 neutrons and the atom after the radiation has taken place has 8 neutrons (1 less). Neutron radiation does not change the number of protons; this is what happened because we had 4 protons before the radiation took place and 4 protons after the radiation took place.
Gamma Radiation
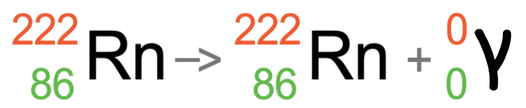
The final example that we are going to look is at radon emitting gamma radiation. Radon will have an atomic number of 86 and a mass number of 222. This means that it has 86 protons and 136 neutrons (222 – 86). Gamma radiation is just energy, which means that it has no mass and no charge; the atomic number and mass number for gamma radiation are both 0. This means that gamma radiation does not change the atomic number and mass number for the atom that is undertaking nuclear decay; the atomic number and mass number remain the same. This means that we get the equation that is shown below.
The final example that we are going to look is at radon emitting gamma radiation. Radon will have an atomic number of 86 and a mass number of 222. This means that it has 86 protons and 136 neutrons (222 – 86). Gamma radiation is just energy, which means that it has no mass and no charge; the atomic number and mass number for gamma radiation are both 0. This means that gamma radiation does not change the atomic number and mass number for the atom that is undertaking nuclear decay; the atomic number and mass number remain the same. This means that we get the equation that is shown below.
End Note
The key rule when balancing nuclear equations is that the numbers for the mass numbers (top numbers) and the atomic numbers (bottom numbers) must be equal on both sides of the equation. It is probably worth writing the equations for each of the different types of radiation on a revision card and then worth looking at the revision card every now and again.
Sometimes it may be the case that an atom is emitting multiple different types of nuclear radiation (e.g. alpha and gamma) and we are asked to write the balanced nuclear equation. We write the nuclear equation by filling in the mass number and atomic number for the types of radiation that are taking place. We then follow the rule that the mass numbers and atomic numbers must be equal on both sides of the equation. There are a few questions like this in the quiz.
The key rule when balancing nuclear equations is that the numbers for the mass numbers (top numbers) and the atomic numbers (bottom numbers) must be equal on both sides of the equation. It is probably worth writing the equations for each of the different types of radiation on a revision card and then worth looking at the revision card every now and again.
Sometimes it may be the case that an atom is emitting multiple different types of nuclear radiation (e.g. alpha and gamma) and we are asked to write the balanced nuclear equation. We write the nuclear equation by filling in the mass number and atomic number for the types of radiation that are taking place. We then follow the rule that the mass numbers and atomic numbers must be equal on both sides of the equation. There are a few questions like this in the quiz.