Back to P5 Home
P5 E) Scale Drawings
P5 E) Scale Drawings
It was fairly easy to find the resultant force acting on an object in the examples in the previous section. This is because the forces were acting in opposite directions; either left and right, or up and down.
However, you may be asked to find the resultant force when there are two or more forces acting on an object along different planes. For example, you may be asked to find the resultant force for an object when there is an upwards and a leftwards force. We can find the resultant force for these types of questions by using scale drawings. We do a scale drawing by drawing a force going from a point. We then draw the next force starting from the end of the first force. It does not matter which force we draw first. Let’s suppose that we are given two forces; one force is upwards, and the other force is rightwards. We can find the resultant force by either drawing the upwards force followed by the rightwards force, or we can draw the rightwards force followed by the upwards force.
When doing scale drawings, we need to use an appropriate scale when we are drawing the forces. For example, if we are working with fairly small forces, 1 cm on our diagram could represent 1 N. However, if we are working with larger forces, 1 cm on the diagram could represent a greater force such as 10 N or 50 N. We will usually have a centimetre grid when answering scale drawing questions in the exam.
After we have drawn the final force, we are able to find the resultant force by measuring the length of the line from where the first force started to where the final force finished. We then use our scale to convert the length into a force. We also measure the bearing of the resultant force line as well. We need to remember these rules when we are working with bearings:
All of this will make a lot more sense after we have gone through a few examples.
However, you may be asked to find the resultant force when there are two or more forces acting on an object along different planes. For example, you may be asked to find the resultant force for an object when there is an upwards and a leftwards force. We can find the resultant force for these types of questions by using scale drawings. We do a scale drawing by drawing a force going from a point. We then draw the next force starting from the end of the first force. It does not matter which force we draw first. Let’s suppose that we are given two forces; one force is upwards, and the other force is rightwards. We can find the resultant force by either drawing the upwards force followed by the rightwards force, or we can draw the rightwards force followed by the upwards force.
When doing scale drawings, we need to use an appropriate scale when we are drawing the forces. For example, if we are working with fairly small forces, 1 cm on our diagram could represent 1 N. However, if we are working with larger forces, 1 cm on the diagram could represent a greater force such as 10 N or 50 N. We will usually have a centimetre grid when answering scale drawing questions in the exam.
After we have drawn the final force, we are able to find the resultant force by measuring the length of the line from where the first force started to where the final force finished. We then use our scale to convert the length into a force. We also measure the bearing of the resultant force line as well. We need to remember these rules when we are working with bearings:
- Bearings are measured from the North line
- Bearings are measured in a clockwise direction
- Bearings are measured in degrees and we always give them as 3 digits
All of this will make a lot more sense after we have gone through a few examples.
Example 1
Click here for a printable PDF of all of the diagrams in this section so that you can give the examples a go as well.
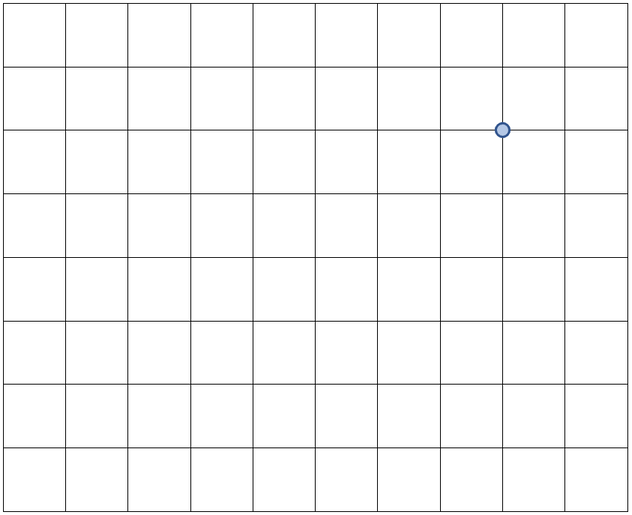
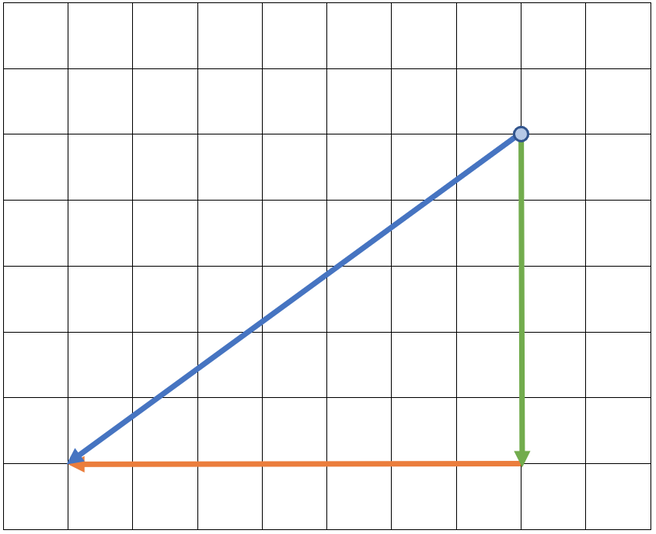
There are two forces acting on a ball; one of the forces is a 3 Newton force in a northwards direction and the other force is a 4 Newton force in an eastwards direction. Find the resultant force acting on the ball. Use the diagram below with the scale 1 cm = 1 N to help you. The blue dot is where the ball starts.
Click here for a printable PDF of all of the diagrams in this section so that you can give the examples a go as well.
There are two forces acting on a ball; one of the forces is a 3 Newton force in a northwards direction and the other force is a 4 Newton force in an eastwards direction. Find the resultant force acting on the ball. Use the diagram below with the scale 1 cm = 1 N to help you. The blue dot is where the ball starts.
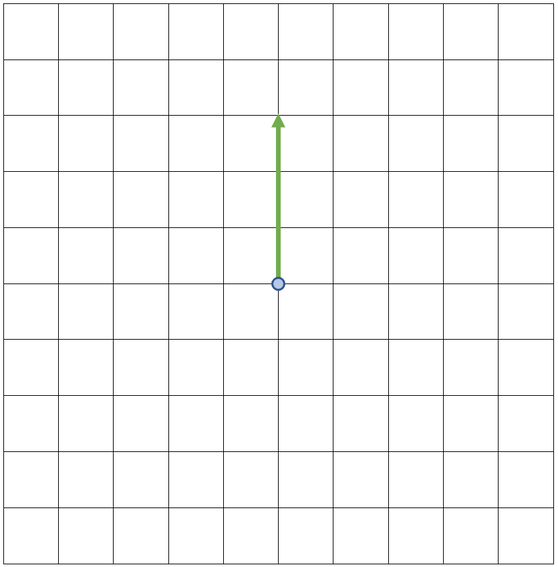
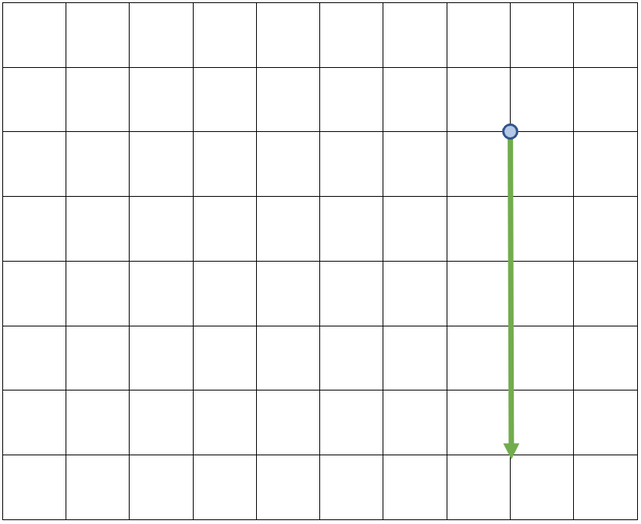
The blue dot on the above diagram shows us where the ball starts. The first step is to draw on one of the forces starting from the blue dot; it does not matter which force we draw on first. I am going to draw the 3 N force in a northwards direction first (north on the diagram will be upwards). The question tells us to use the scale 1 cm = 1 N. The northwards force is 3 N, which means that the northwards force will be 3 cm long. I have added this force to the scale diagram.
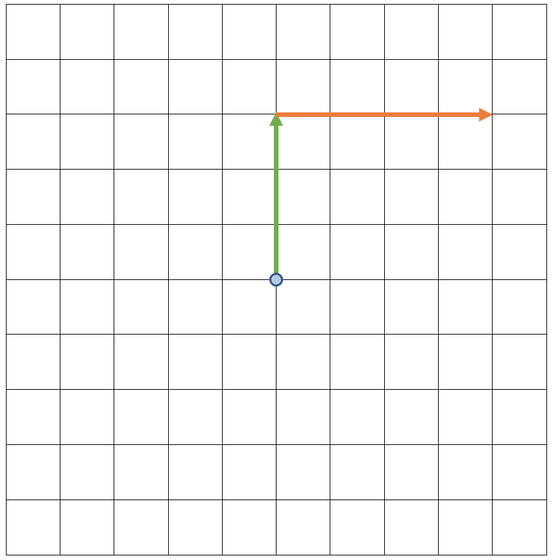
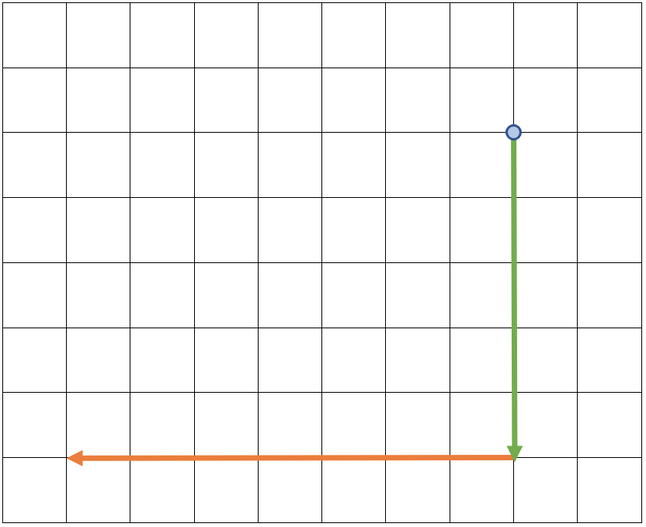
The next step is to draw the second force on the diagram starting from where the first force ended. The second force is a 4 N force in an eastwards direction, which will be towards the right on the scale diagram. The scale on the scale diagram is still 1 cm = 1 N, so this force will be 4 cm. I have added this force to the scale diagram.
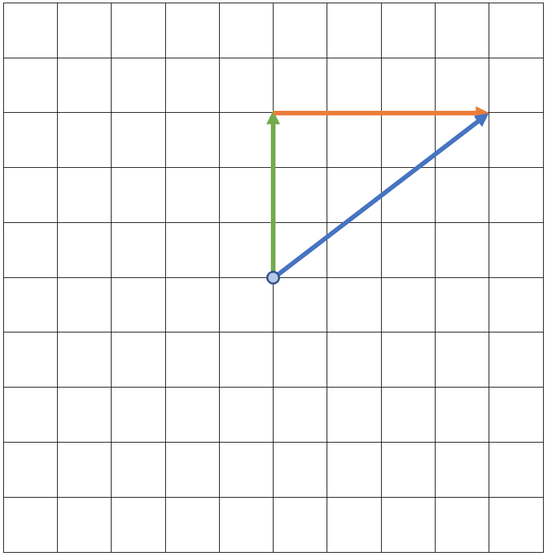
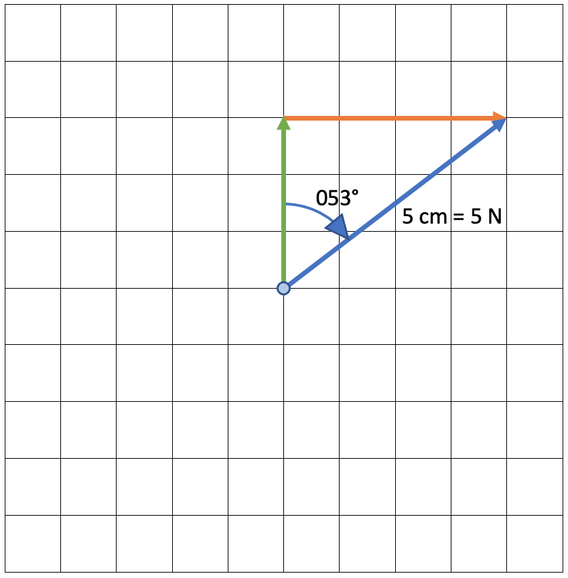
We now have both of the forces on the diagram. The resultant force goes from the initial starting point (the blue dot) to the end of the final force. The resultant force is shown on the diagram below (the blue arrow).
We now need to work out the magnitude and the bearing of the resultant force.
We work out the magnitude of the resultant force by measuring the length of the blue line and converting the length into a force by using the scale. The length of the resultant force on our scale diagram is 5 cm. The scale that we used is 1 cm = 1 N, and this means that our resultant force is 5 N.
The next step is to work out the bearing of the resultant force. Bearings are always measured clockwise from the north line (up) and are given as three-digit numbers. The working for the bearing is shown below.
We work out the magnitude of the resultant force by measuring the length of the blue line and converting the length into a force by using the scale. The length of the resultant force on our scale diagram is 5 cm. The scale that we used is 1 cm = 1 N, and this means that our resultant force is 5 N.
The next step is to work out the bearing of the resultant force. Bearings are always measured clockwise from the north line (up) and are given as three-digit numbers. The working for the bearing is shown below.
The bearing is 053° (remember, we always give bearings as three-digit numbers).
So, the resultant force is 5 N on a bearing of 053°.
So, the resultant force is 5 N on a bearing of 053°.
Example 2
Two forces are acting on a ship; one of the forces is a 500 Newton force in a southwards direction and the other force is a 700 Newton force in a westwards direction. Find the resultant force acting on the ship. Use the diagram below to help you – the starting position of the ship is the blue dot.
Two forces are acting on a ship; one of the forces is a 500 Newton force in a southwards direction and the other force is a 700 Newton force in a westwards direction. Find the resultant force acting on the ship. Use the diagram below to help you – the starting position of the ship is the blue dot.
The first step is to draw on one of the forces starting from the blue dot; it does not matter which force we draw on first. I am going to draw the 500 N force in a southwards direction first (south on the diagram will be downwards). The question does not give us a scale to use, which means that we must come up with an appropriate scale; I am going to use the scale 1 cm = 100 N. This means that the 500 N southwards force will be 5 cm on the scale diagram (500 ÷ 100 = 5). The 500 N southwards force is shown on the diagram below.
The next step is to draw the second force on the diagram starting from where the first force ended. The second force is a 700 N force in a westwards direction, which is towards the left on the scale diagram. The scale that we used earlier was 1 cm = 100 N, and this means that the 700 N force will be 7 cm (700 ÷ 100 = 7). I have added this force to the scale diagram.
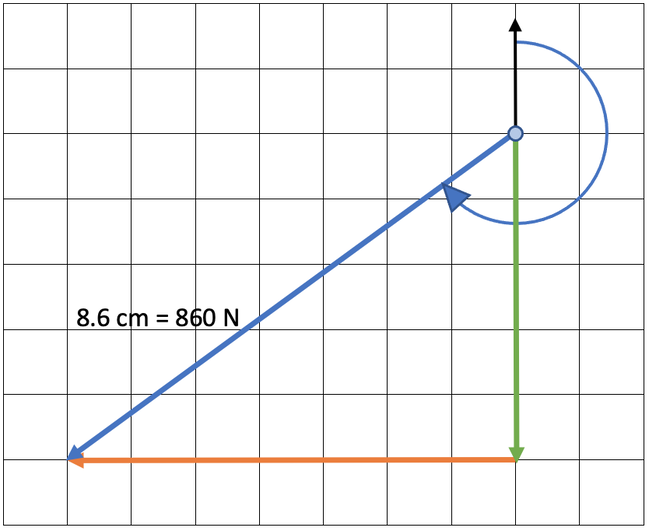
We now have both of the forces on the diagram. The resultant force goes from the initial starting point (the blue dot) to the end of the final force. The resultant force is shown on the diagram below (the blue arrow).
We now need to work out the magnitude and the bearing of the resultant force.
We work out the magnitude of the resultant force by measuring the length of the blue line and converting the length into a force by using the scale. The length of the resultant force on our scale diagram is 8.6 cm. The scale that we used is 1 cm = 100 N, and this means that our resultant force is 860 N (8.6 x 100 = 860).
The next step is to work out the bearing of the resultant force. Bearings are always measured clockwise from the north line (up) and are given as three-digit numbers. I have added a north line and an arrow showing the bearing for the resultant force.
We work out the magnitude of the resultant force by measuring the length of the blue line and converting the length into a force by using the scale. The length of the resultant force on our scale diagram is 8.6 cm. The scale that we used is 1 cm = 100 N, and this means that our resultant force is 860 N (8.6 x 100 = 860).
The next step is to work out the bearing of the resultant force. Bearings are always measured clockwise from the north line (up) and are given as three-digit numbers. I have added a north line and an arrow showing the bearing for the resultant force.
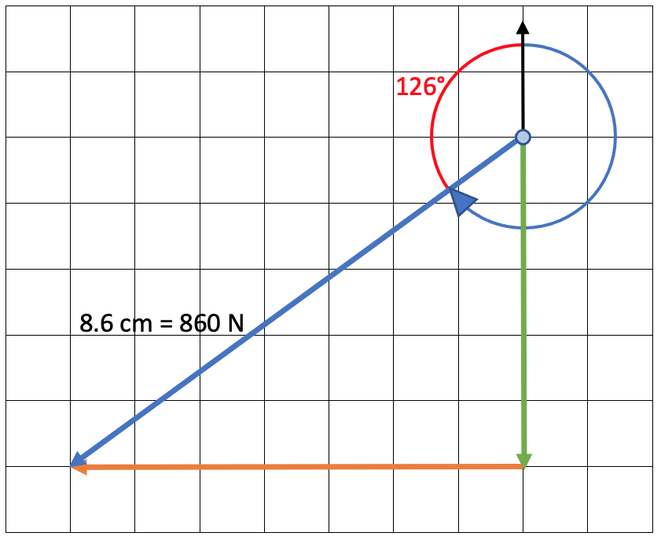
The easiest way to work out the bearing for bearings above 180°, is to measure the angle anticlockwise between the north line and the bearing line. We then take this angle from 360° (a full turn) to work out the bearing.
The anticlockwise angle between the north line and the resultant force is 126°. We then take away from 360°.
The bearing is 234°.
We now have our answer; the resultant force is 860 N on a bearing of 234°.
There will be a range of acceptable answers for resultant forces and bearings from scale diagrams. For this question the range of acceptable answers could have been a resultant force between 830 N and 890 N, and the bearing could have been between 229° and 239°.
We now have our answer; the resultant force is 860 N on a bearing of 234°.
There will be a range of acceptable answers for resultant forces and bearings from scale diagrams. For this question the range of acceptable answers could have been a resultant force between 830 N and 890 N, and the bearing could have been between 229° and 239°.
Equilibrium
An object is in an equilibrium if it has a resultant force of zero. An object in equilibrium will continue with the same state of motion. A stationary object in equilibrium will remain stationary. A moving object in equilibrium will continuing moving at exactly the same velocity (speed in a particular direction).
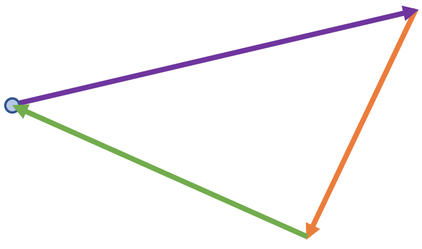
We can use scale drawings to see if an object is in equilibrium (has a resultant force of zero). We do this by drawing all of the forces acting on an object tip to tail (the order that we draw the forces does not matter). If all of the forces lead back to the starting point, it means that there is a resultant force of zero, thus meaning that the object is in an equilibrium. Here is an example.
Example
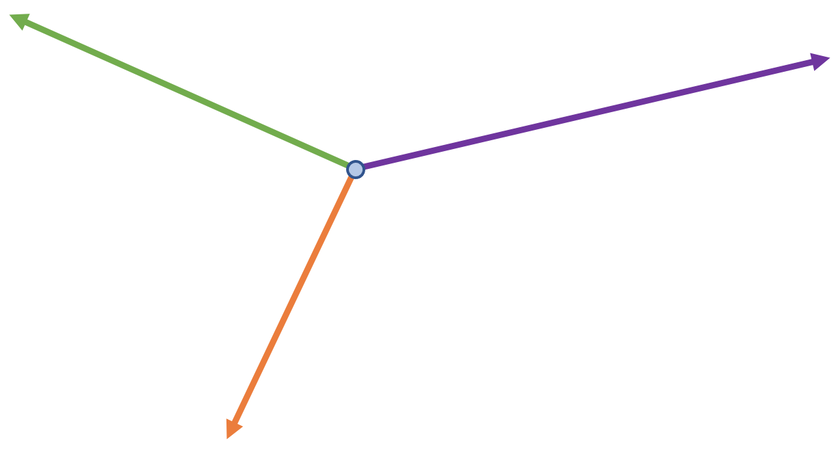
There are three forces acting on the object below. Show that the resultant force is zero.
An object is in an equilibrium if it has a resultant force of zero. An object in equilibrium will continue with the same state of motion. A stationary object in equilibrium will remain stationary. A moving object in equilibrium will continuing moving at exactly the same velocity (speed in a particular direction).
We can use scale drawings to see if an object is in equilibrium (has a resultant force of zero). We do this by drawing all of the forces acting on an object tip to tail (the order that we draw the forces does not matter). If all of the forces lead back to the starting point, it means that there is a resultant force of zero, thus meaning that the object is in an equilibrium. Here is an example.
Example
There are three forces acting on the object below. Show that the resultant force is zero.
We can show that the resultant force is zero by drawing the forces tip to tail to each other on the diagram; the order that we draw the forces does not matter.
From the above diagram, we can see that the forces lead back to the starting point. This means that the resultant force is zero and the object is in an equilibrium.
Splitting a Resultant Force
We can split a resultant force at an angle into two separate forces; a horizontal force and a vertical force. These two separate forces acting together have the same effect as the single resultant force. The reason why we may want to split the resultant force into two separate forces is because having two separate forces makes it easier to solve certain calculations. We find the vertical and horizontal forces by creating a triangle from the resultant force on the scale diagram. Let’s have an example.
Example
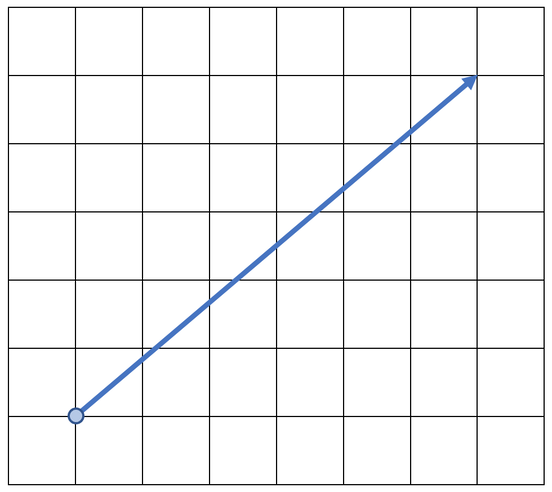
Split the resultant force on the scale diagram below into a horizontal and vertical force. The scale is 1 cm = 2 N and each square is 1 cm. Give the direction of the forces in terms of north, east, south and west.
We can split a resultant force at an angle into two separate forces; a horizontal force and a vertical force. These two separate forces acting together have the same effect as the single resultant force. The reason why we may want to split the resultant force into two separate forces is because having two separate forces makes it easier to solve certain calculations. We find the vertical and horizontal forces by creating a triangle from the resultant force on the scale diagram. Let’s have an example.
Example
Split the resultant force on the scale diagram below into a horizontal and vertical force. The scale is 1 cm = 2 N and each square is 1 cm. Give the direction of the forces in terms of north, east, south and west.
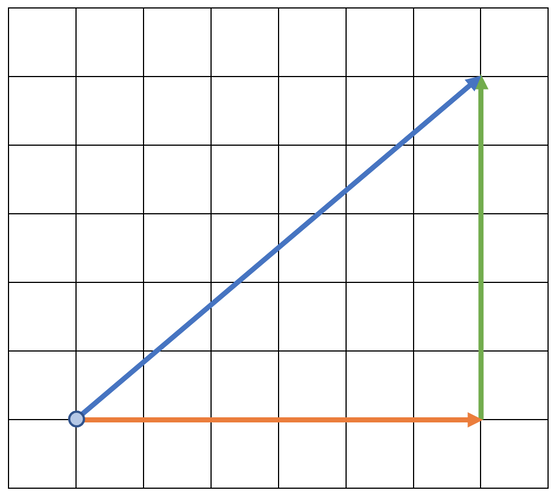
I am going to create a triangle to show the horizontal and vertical components of the resultant force.
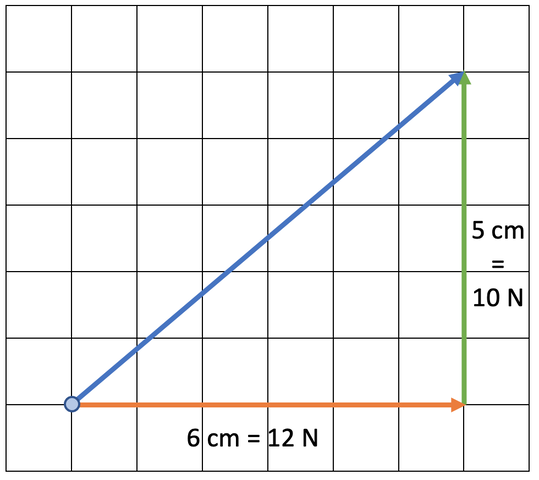
The scale for the diagram is 1 cm = 2 N.
The horizontal component is 6 cm long, which represents a force of 12 N (6 x 2 = 12). The horizontal force is going towards the right, which means that it is acting in an eastwards direction.
The vertical component is 5 cm long, which represents a force of 10 N (5 x 2 = 10). The vertical force is going upwards, which means that it is acting in a northwards direction.
The horizontal component is 6 cm long, which represents a force of 12 N (6 x 2 = 12). The horizontal force is going towards the right, which means that it is acting in an eastwards direction.
The vertical component is 5 cm long, which represents a force of 10 N (5 x 2 = 10). The vertical force is going upwards, which means that it is acting in a northwards direction.
Therefore, this resultant force as a horizontal and vertical force can be represented as a force of 12 N in an eastwards direction and a force of 10 N in a northwards direction.