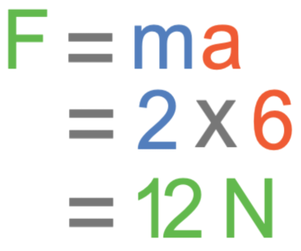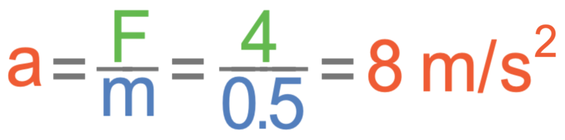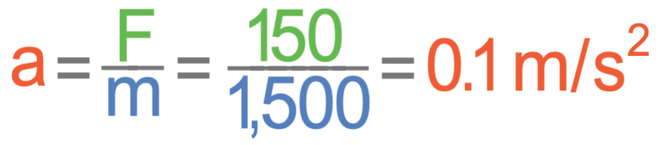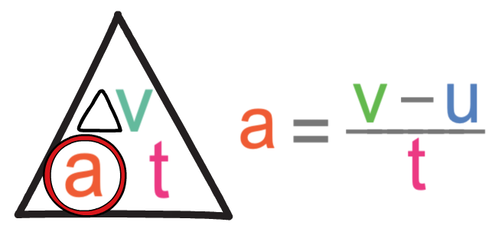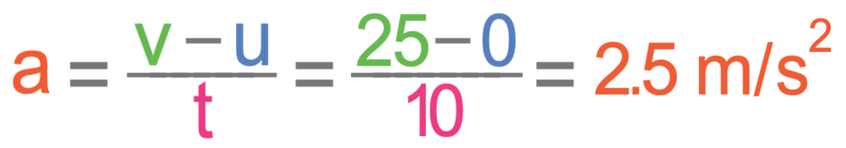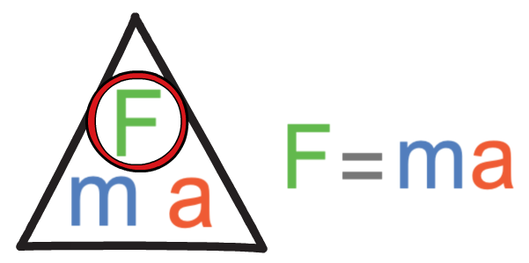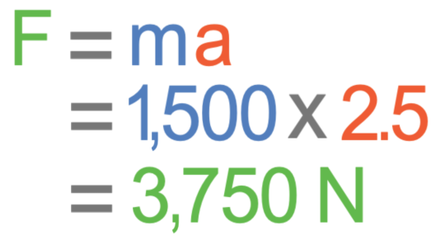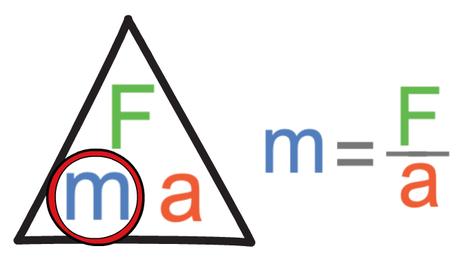P5 Q) Newton’s First & Second Law
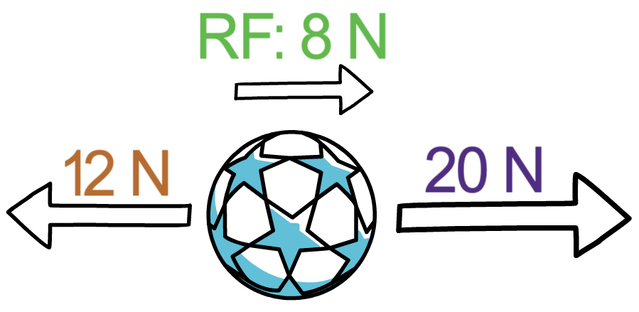
Newton’s first laws states that a resultant force is needed to make an object start moving, speed up or slow down. If the resultant force acting on an object is zero, the object will remain in the same condition.
Stationary
If the object is stationary, a resultant force of zero means that the object will remain stationary.
Moving
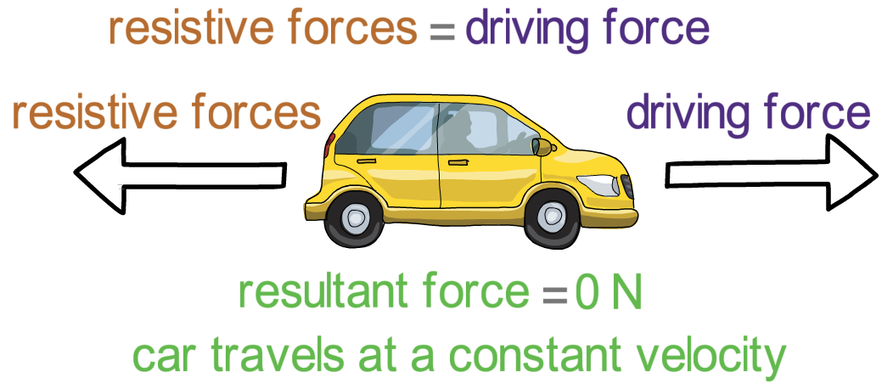
If the object is moving, a resultant force of zero means that the object will continue moving at exactly the same velocity; for example, if a car is travelling at a velocity of 25 m/s and the resultant force is zero, the car will continue travelling at a velocity of 25 m/s.
When a car or any other object is travelling at a constant velocity, the driving force and resistive forces balance out resulting in the resultant force being zero. The resistive forces for the car below will be air resistance and friction.
Newton’s first law then goes on to say that the velocity of an object will only change when there is a non-zero resultant force acting on an object. The object will then accelerate in the direction of the resultant force. This acceleration can take 5 different forms:
- Starting
- Stopping
- Speeding up
- Slowing down
- Changing direction
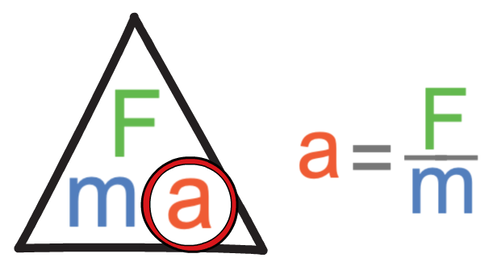
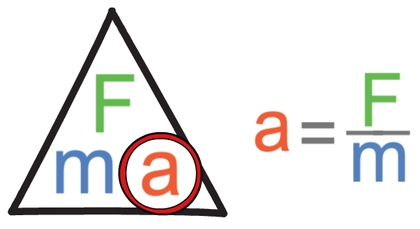
Newton’s second law states that the acceleration of an object is determined by the resultant force acting on an object and the mass of the object. The equation for this is shown below.
In the above equation, the resultant force is measured in Newtons (N), mass is measured in kilograms (kg) and acceleration is measured in metres per second squared (m/s2).
The resultant force and acceleration are directly proportional to one another – an increase in the resultant force results in an increase in acceleration, and a decrease in the resultant force results in a decrease in acceleration.
The acceleration and mass are inversely proportional to one another. For the same resultant force, an increase in mass would result in a decrease in acceleration (or vice versa). For example, if you were to kick a bowling ball and a football as hard as you can, the football will accelerate at a greater rate because the football has a smaller mass compared to the bowling ball.
Let’s now have a few calculation examples.
Example 1
A ball has a mass of 2 kg and an acceleration rate of 6 m/s2. Find the resultant force acting on the ball.
We find the resultant force acting on the ball by using the formula below.
The question tells us that the mass of the ball is 2 kg and the acceleration is 6 m/s2. Both of these values are in the correct units, so we can sub them straight into the formula.
The resultant force is 12 N.
Example 2
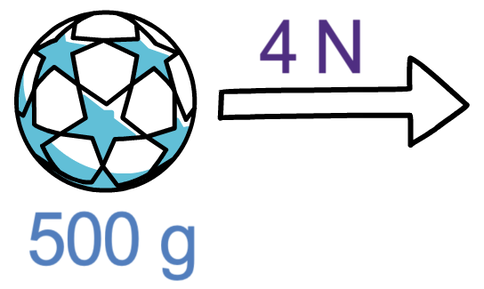
The stationary ball below has a mass of 500 grams and there is a resultant force of 4 N acting on the ball towards the right. Find the acceleration of the ball and the direction of acceleration.
The resultant force acting on the ball is towards the right, which means that the ball will accelerate towards the right. We now need to find the acceleration rate, which we do by dividing the resultant force in newtons by the mass in kilograms.
The resultant force is 4 N, which is in the correct units. The mass is 500 grams, which is not in the correct units as the mass should be in kilograms and not grams. We convert grams to kilograms by dividing by 1000, which means that the mass in kilograms is 0.5 kg (500 ÷ 1000 = 0.5). We now sub the force in as 4 and the mass in as 0.5.
Therefore, the acceleration is 8 m/s2 towards the right.
Example 3
We are now going to have a look at an example whereby we need to work out the resultant force acting on an object before we are able to work out the acceleration of the object. It is always worth drawing a diagram for these types of questions.
Question
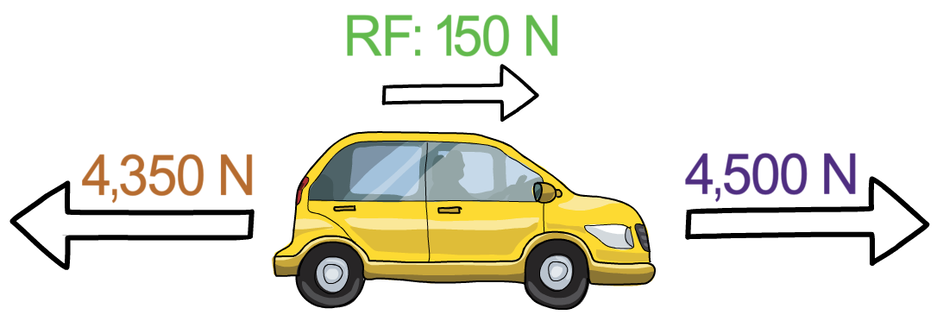
A car has a mass of 1,500 kg and its engine is providing a driving force of 4,500 N. When the car is travelling at 30 m/s, the car experiences 4,350 N of resistive forces (air resistance and friction). Work out the acceleration of the car when it is travelling at 30 m/s.
The first step in answering this question is to work out the resultant force. It is easier to work out the resultant force by drawing a diagram. I am going to say that the car is travelling towards the right and this means that the driving force of 4,500 N will be towards the right. The resistive forces will act in the opposite direction to the direction of travel; the resistive forces will be towards the left – we draw a leftwards arrow with 4,350 N on top.
We now work out the resultant force. The driving force (4,500 N) is bigger than the resistive forces (4,350 N). This means that the resultant force will be towards the right and the resultant force is 150 N (4,500 – 4,350 = 150). I have added this to the diagram below.
So, there is a resultant force of 150 N to the right.
We can now work out the acceleration of the car. We work out acceleration by dividing the resultant force by the mass.
The resultant force is 150 N and the mass of the car is 1,500 kg. These values are in the correct units, so we sub them into the formula.
We worked out our resultant force towards the right and we took the right as the direction of travel. This means that the car is accelerating, and the acceleration is 0.1 m/s2.
Example 4
We are now going to have a look at an estimation question. Like all estimation questions, we use typical values or realistic values.
Question
Estimate the resultant force acting on a car as it accelerates from rest to a typical speed.
We are going to use two different calculations to answer this question.
Calculation 1
The first calculation is to estimate the acceleration of the car. The question tells us that the car is accelerating from rest to a typical speed. Rest means that the car is stationary (it has a speed of 0 m/s). A typical speed of a car is 25 m/s. I would say that it takes around 10 seconds for a car to reach this speed. The formula triangle and calculation for acceleration is shown below.
The change in velocity is 25 m/s (v – u = 25 – 0 = 25), and the time is 10 seconds. We sub these values into the formula.
This tells us that the acceleration is 2.5 m/s2.
Calculation 2
The next calculation is Newton’s second law, which we use to find the resultant force acting on the car. The calculation for Newton’s second law is shown below.
We found that the acceleration of the car is 2.5 m/s2. We now need to estimate the mass of the car; a typical car has a mass of around 1,500 kg. We sub these values into the formula.
Therefore, an estimate for the resultant force acting on a car when it accelerates from rest to a typical speed is around 3,750 newtons.
The law of inertia states that the motion of an object will remain the same unless a resultant force acts on the object (Newton’s first law). This can take 2 forms:
- If the object is stationary, the object will remain stationary unless a resultant force acts on the object.
- If the object is moving, the object will continue moving at exactly the same velocity unless a resultant force acts on the object.
An object’s inertia mass is a measure of how difficult it is to change the velocity of an object. We find the calculation for inertia mass by rearranging Newton’s second law (F = ma) to make mass the subject. The equation for inertia mass is shown below