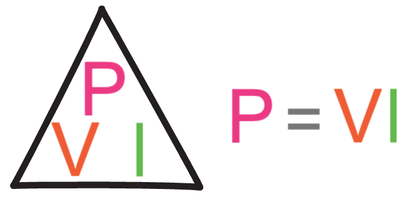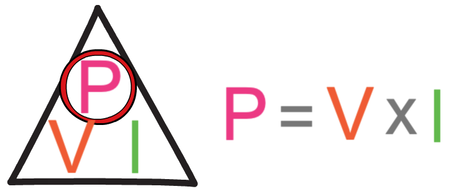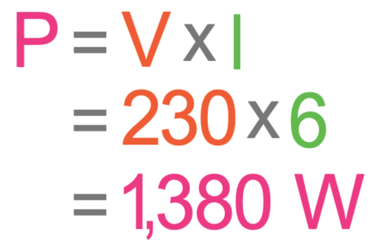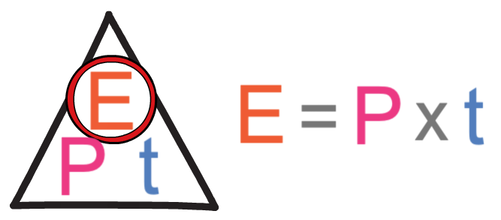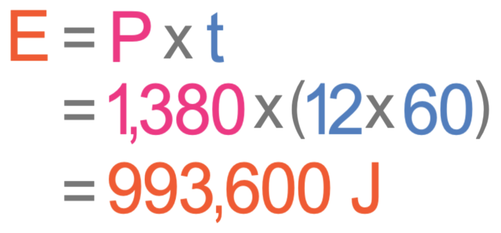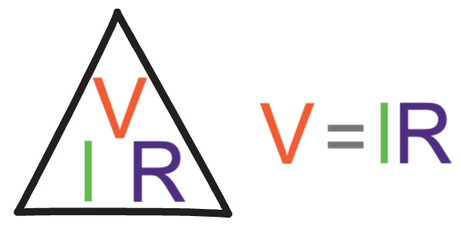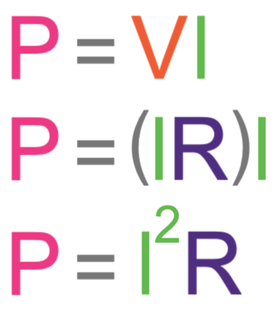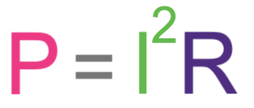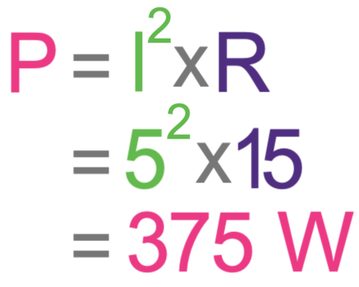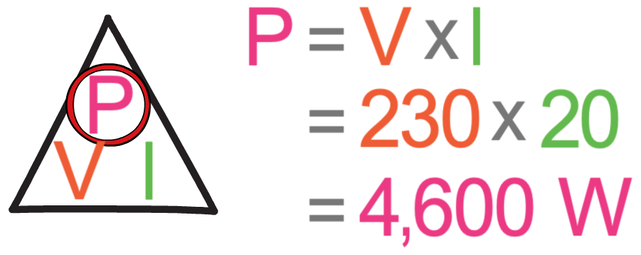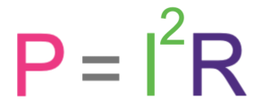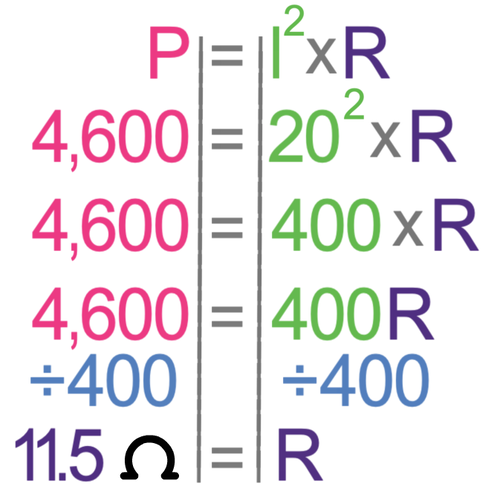Power is the amount of energy that a device transfers per second. We can work out the power of an electrical appliance by multiplying the potential difference by the current.
Power is measured in watts (W), current is measured in amps (A) and potential difference is measured in volts (V). Let’s have an example.
Example 1
An electric heater that is plugged into the mains has a current of 6 A. Find the power of the electric heater.
We can find the power of the electric heater by multiplying the potential difference by the current.
An electric heater that is plugged into the mains has a current of 6 A. Find the power of the electric heater.
We can find the power of the electric heater by multiplying the potential difference by the current.
The question tells us that the electric heater is plugged into the mains. Mains electricity has a potential difference of 230 V, so V is 230 V. We are also told in the question that the current is 6 A. We sub these values into the power calculation.
The power of the electric heater is 1,380 W.
Extension
We could extend this question by finding the energy transfer is the heater is on for a certain period of time. For example, how much energy is transferred if the heater is on for 12 minutes.
We find the energy transfer by multiplying the power (in watts) by the time (in seconds). The formula is shown below.
Extension
We could extend this question by finding the energy transfer is the heater is on for a certain period of time. For example, how much energy is transferred if the heater is on for 12 minutes.
We find the energy transfer by multiplying the power (in watts) by the time (in seconds). The formula is shown below.
We have just found out that the power of the electric heater is 1,380 W and we are told in the extension question that the time is 12 minutes. The time needs to be in seconds, so when we sub time into the equation, we need to multiply it by 60 as there are 60 seconds in 1 minute.
The energy transfer when the electric heater is on for 12 minutes is 993,600 joules (or 993.6 KJ).
Rearranging the Formula
The formula for power is shown below.
The formula for power is shown below.
V in the above formula is potential difference. We can work out the potential difference by multiplying the current by the resistance (V = IR); this was one of the first electricity formulas that we looked at.
We are able to sub IR in for V into the power equation and manipulate the equation to get what is shown below.
This means that we are able to work out the power of a device even if we are not given the potential difference.
Example 2
A device has a current of 5 A and a resistance of 15 Ω. Find the power of the device.
We are not given the potential difference in the question, which means that we work out the power of the device by using the power formula without potential difference; this formula is shown below.
A device has a current of 5 A and a resistance of 15 Ω. Find the power of the device.
We are not given the potential difference in the question, which means that we work out the power of the device by using the power formula without potential difference; this formula is shown below.
We are told in the question that the current is 5 A and the resistance is 15 Ω. Both of these are in the correct units, so we just sub them into the equation.
The power of the device is 375 W.
Example 3
The next example that we will look at will require us to use two of the power formulas. There is a fair amount of working for this question and it will be about 4 or 5 marks.
A device is connected to the mains and it has a current of 20 A. Calculate the power and the resistance of the device.
The device is connected to the mains, which means that the potential difference of the device is 230 V. We can work out the power of the device by multiplying the potential difference (230 V) by the current (20 A).
The next example that we will look at will require us to use two of the power formulas. There is a fair amount of working for this question and it will be about 4 or 5 marks.
A device is connected to the mains and it has a current of 20 A. Calculate the power and the resistance of the device.
The device is connected to the mains, which means that the potential difference of the device is 230 V. We can work out the power of the device by multiplying the potential difference (230 V) by the current (20 A).
The power of the device is 4,600 watts.
We now use the other power formula that contains resistance. This formula is shown below.
We now use the other power formula that contains resistance. This formula is shown below.
We have just found the power of the device (4,600 W) and the question tells us that the current is 20 A. We sub these values into the formula and solve to find the resistance. The working is shown below.
The resistance of the device is 11.5 Ω.
So, the power of the device is 4,600 W and the resistance of the device is 11.5 Ω.
So, the power of the device is 4,600 W and the resistance of the device is 11.5 Ω.