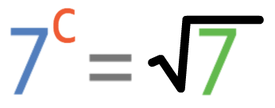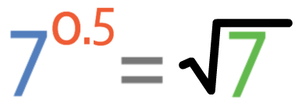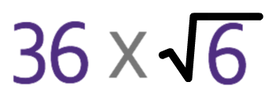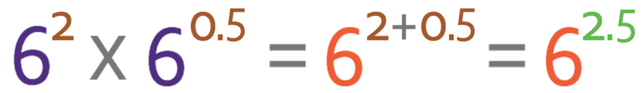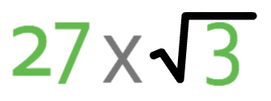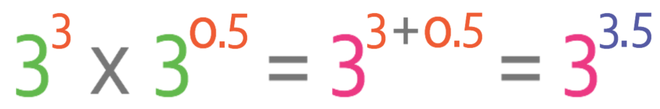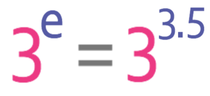Back to AQA Indices (F) Home
​​​1.6 H) Putting Numbers into Indices – Part 2
The content in this section builds on the content that was discussed in the previous section. Before working through this section, make sure that you have covered the content in the previous section (click here to be taken to the previous section).
Surds
Another way that these questions can be made more complex is to have surds involved. The power for a square root is ½ or 0.5.

So, if we had the equation below:
The value of c would be ½ or 0.5.
​We are now going to have a look at an example whereby a surd will be multiplied by something.
Example 1
We have the equation below:
Find the value of d.
 
This question is essentially saying “6 to the power of what gives us 36√6”. I am going to answer this question by working with the right side of the equation. Currently, the right side of the equation is saying 36 lots of √6. This means that we can add in a multiplication sign between the two terms to get:

The adding in of the multiplication sign on the right side of the equation makes it easier to work with and you will see why in a few steps time. We now need to write each of the terms (36 and √6) in the form of the base number on the left side of the equation to the power of something. The base number on the left side of the equation is 6. Therefore, we are going to write 36 and √6 as 6something; 36 when written as 6something is 62, and √6 when written as 6something is 60.5 (or 6½). This results in the right side of the equation becoming:

​We can now use the multiplication rules for powers, which is that when we are multiplying powers that have the same base, we add the powers (this is the reason for adding in the multiplication sign between the two terms). The bases for the powers are both 6, which means that we can add 2 and 0.5 together.
We can now combine this with the left side of the equation to give us the equation:
​This means that d is 2.5.
Example 2
We have the equation:
Find the value of e.
 
Like the previous example, I am just going to work with the right side of the equation. The right side of the equation is saying 27 lots of √3, and this means that we can add in a multiplication sign between the two terms. This results in the right side of the equation becoming:

We now need to write each of the terms (27 and √3) in the form of the base number on the left side of the equation to the power of something. The base number on the left side of the equation is 3. Therefore, we are going to write 27 and √3 as 3something; 27 when written as 3something is 33, and √3 when written as 3something is 30.5 (or 3½). This results in the right side of the equation becoming:

​We can now use the multiplication rule for powers, which is that when we are multiplying powers with the same base, we add the powers. The bases for both of the powers are 3, which means that we add the power; we add 3 and 0.5 to get 3.5.
We can now combine this with the left side of the equation to give us the equation:
This means that e is 3.5.