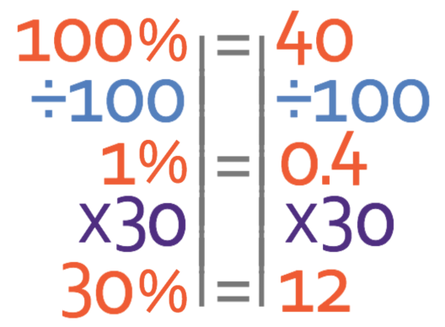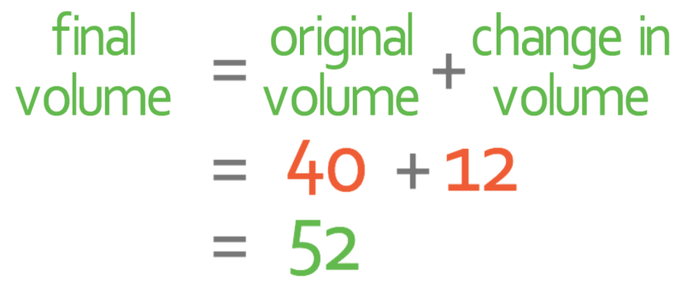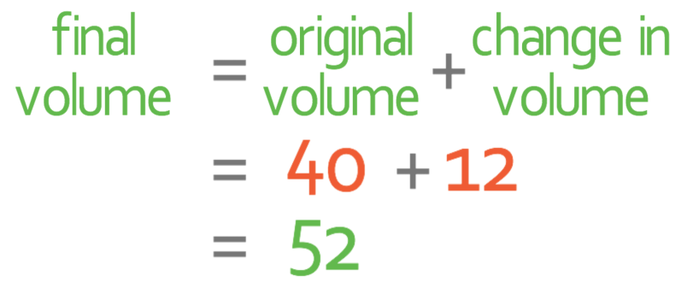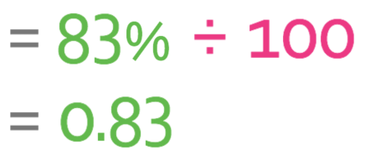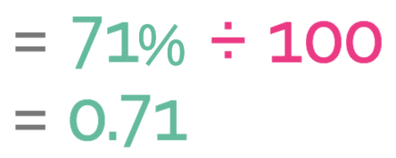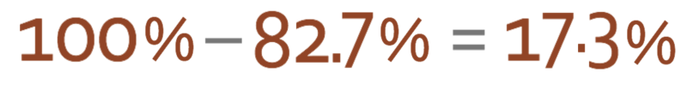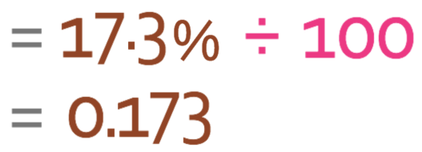Back to AQA Percentages (F) Home
3.2 H) Increasing or Decreasing by a Certain Percentage – Calculator: Part 1
3.2 H) Increasing or Decreasing by a Certain Percentage – Calculator: Part 1
In this section we are going to be looking at increasing or decreasing an amount by a certain percentage when we are able to use a calculator. Some of the examples in this section are the same as the examples in the previous section. Before you work through this section, make sure that you have worked through the previous section (click here to be taken through to the previous section).
Example 1
The first example in the previous section was the placing of 40 cubic centimetres of dough into a fridge to rise. After 20 minutes, the volume of the dough increased by 30%. What is the volume of dough after 20 minutes?
There are three different methods that we can use when we are using a calculator to find what 30% of 40 cubic centimetres is.
Method 1
The first method is to divide 40 by 100 to find out what 1 % equals. When we do this, we see that 1% is 0.4. The next step is to multiply this value by 30, so that we have the value for 30%, which gives us 12.
The first example in the previous section was the placing of 40 cubic centimetres of dough into a fridge to rise. After 20 minutes, the volume of the dough increased by 30%. What is the volume of dough after 20 minutes?
There are three different methods that we can use when we are using a calculator to find what 30% of 40 cubic centimetres is.
Method 1
The first method is to divide 40 by 100 to find out what 1 % equals. When we do this, we see that 1% is 0.4. The next step is to multiply this value by 30, so that we have the value for 30%, which gives us 12.
The final step is to add what we have found to our original answer; we add because we are told that the volume of the dough increases. Therefore, we add 12 to 40, which tells us that the final volume of the dough is 52 cubic centimetres.
Method 2
The second method when using a calculator is to convert the percentage that we are looking for into a decimal. We then multiply the decimal that we have just obtained by the original volume (40 cubic centimetres) to find what 30% would be. To convert 30% into a decimal, we divide by 100, which gives us 0.3. We then multiply 0.3 by 40 cubic centimetres, which is 12 cubic centimetres.
The second method when using a calculator is to convert the percentage that we are looking for into a decimal. We then multiply the decimal that we have just obtained by the original volume (40 cubic centimetres) to find what 30% would be. To convert 30% into a decimal, we divide by 100, which gives us 0.3. We then multiply 0.3 by 40 cubic centimetres, which is 12 cubic centimetres.
The final step is to add on what 30% is to the original volume, which gives us 52 cubic centimetres.
Method 3 – Multiplier Method
The third method is known as the multiplier method. This method is quicker than the previous two methods as it skips out a few steps on the calculator. It is an extremely useful method in financial mathematics (such as interests).
In the dough example above, we were increasing the volume of our dough; we were adding 30% of the original volume of the dough to find the final volume of the dough. We are able to find out what the multiplier is from this information. We are adding 30% to the original volume and the original volume represents 100%. Therefore, the final volume in percentage terms is:
The third method is known as the multiplier method. This method is quicker than the previous two methods as it skips out a few steps on the calculator. It is an extremely useful method in financial mathematics (such as interests).
In the dough example above, we were increasing the volume of our dough; we were adding 30% of the original volume of the dough to find the final volume of the dough. We are able to find out what the multiplier is from this information. We are adding 30% to the original volume and the original volume represents 100%. Therefore, the final volume in percentage terms is:
The final volume in percentage form is 130%. To obtain the multiplier value, we need to convert this percentage into a decimal, which we do by dividing by 100.
Our multiplier value is 1.3. The final step is to multiply our initial value by the multiplier that we have found.
Therefore, the final volume of the dough is 52 cubic centimetres.
The Rules
If we are increasing our value by a percentage, we always add the percentage change onto 100%, then divide by 100 to obtain our multiplier. If we are decreasing our value by a percentage, we take the percentage decrease from 100%, and then divide by 100 to obtain the multiplier.
If we are increasing our value by a percentage, we always add the percentage change onto 100%, then divide by 100 to obtain our multiplier. If we are decreasing our value by a percentage, we take the percentage decrease from 100%, and then divide by 100 to obtain the multiplier.
Multiplier – Increasing
Let’s have find the multiplier value for a few more percentage increases.
Multiplier Example 1
What is the multiplier value if we were to increase our value by 73%?
We are increasing our value, so we are going to be adding 73% to our original value (the original value represents 100%).
Let’s have find the multiplier value for a few more percentage increases.
Multiplier Example 1
What is the multiplier value if we were to increase our value by 73%?
We are increasing our value, so we are going to be adding 73% to our original value (the original value represents 100%).
Therefore, our final value will be 173% of the original value (100% + 73%). We now need to convert 173% from a percentage to a decimal and we do this by dividing by 100.
The multiplier is 1.73.
Multiplier Example 2
What is the multiplier value if we are to increase our value by 4.5%?
As we are increasing our value, we add the percentage increase (4.5%) on to 100%.
What is the multiplier value if we are to increase our value by 4.5%?
As we are increasing our value, we add the percentage increase (4.5%) on to 100%.
This means that the final percentage is 104.5% (100% + 4.5%). To obtain our multiplier, we then divide our percentage by 100.
The multiplier is 1.045.
Multiplier – Decreasing
If we are decreasing our value by a percentage we take the percentage decrease from 100%, and then divide by 100 to obtain the multiplier value.
We are going to use the multiplier method to answer the second example on the previous section. The question was:
I leave a glass that contains 350 ml of water in the sun for 20 minutes. During this time, 17% of the water evaporates. How much water is left in the container?
The amount of water is decreasing, and it is decreasing by 17%. To obtain the multiplier, we take the percentage that the volume of water is decreasing from 100.
If we are decreasing our value by a percentage we take the percentage decrease from 100%, and then divide by 100 to obtain the multiplier value.
We are going to use the multiplier method to answer the second example on the previous section. The question was:
I leave a glass that contains 350 ml of water in the sun for 20 minutes. During this time, 17% of the water evaporates. How much water is left in the container?
The amount of water is decreasing, and it is decreasing by 17%. To obtain the multiplier, we take the percentage that the volume of water is decreasing from 100.
We now need to convert this into a multiplier value and we do this by dividing by 100.
We now have the multiplier and the original volume of water in the glass, which was 350 ml. To obtain the final volume of water in the glass, we multiply the original amount of water in the glass (350 ml) by our multiplier value (0.83).
The volume of water after 20 minutes in the sun is 290.5 ml.
Let’s have a few more example of finding multipliers when values are decreasing by a certain percentage.
Multiplier Example 3
What is the multiplier value if we are decreasing something by 29%?
We are decreasing our value by 29%, which means that we need to take away 29% from 100%.
Multiplier Example 3
What is the multiplier value if we are decreasing something by 29%?
We are decreasing our value by 29%, which means that we need to take away 29% from 100%.
This gives us 71%. We turn this into a multiplier by dividing by 100.
The multiplier is 0.71.
Multiplier Example 4
What is the multiplier value if we were to decrease our value by 82.7%?
As we are decreasing our value by 82.7%, we need to take away 82.7% from 100%.
What is the multiplier value if we were to decrease our value by 82.7%?
As we are decreasing our value by 82.7%, we need to take away 82.7% from 100%.
This gives us a 17.3%. To obtain the multiplier, we then divide by 100.
The multiplier is 0.173.