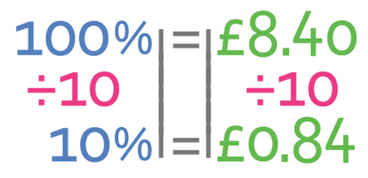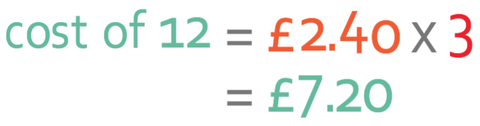Back to AQA Unit of Measure (F) Home
4.10 H) Unit Pricing Involving Offers
4.10 H) Unit Pricing Involving Offers
We are now going to have a look at some best buy questions that involve offers, such as buy one get one free or get 20% off. We will then be asked to purchase a certain number of the goods. In the first example, we will only be able to purchase the whole quantity from one of the shops. In the second example, we will be able to purchase any quantity from any of the shops. Let’s have a few examples.
Example 1
Do not use a calculator for this question.
There are two different shops that I can purchase orange juice from. The price and offers for the two shops are shown below:
I want to purchase 12 cartons of orange juice and I can only purchase from one of the shops. Where should I purchase the orange juice from?
We are told in the question that we are only able to purchase orange juice from one of the shops. Therefore, the easiest way to answer a question like this is to find out the total cost for the 12 cartons from both of the shops. Let’s start with shop 1.
Shop 1
Cartons are 70p from shop 1 and they have an offer where you get 20% off. We want to find the total cost and there are two different ways that we can do this. The first way is to find the total cost of the 12 cartons at full price, and then take the 20% off. The second method is to take 20% off of the price of one carton, and then multiply the sale price by the number of cartons (12).
I am going to use the first method. We find the cost of 12 cartons by multiplying 70p (the cost of 1 carton) by 12.
Do not use a calculator for this question.
There are two different shops that I can purchase orange juice from. The price and offers for the two shops are shown below:
- Shop 1 sells orange juice for 70p and they currently have an offer whereby you get 20% off.
- Shop 2 sells orange juice for 80p and they currently have an offer whereby you if you buy 3 cartons of orange juice, you get the 4th carton free.
I want to purchase 12 cartons of orange juice and I can only purchase from one of the shops. Where should I purchase the orange juice from?
We are told in the question that we are only able to purchase orange juice from one of the shops. Therefore, the easiest way to answer a question like this is to find out the total cost for the 12 cartons from both of the shops. Let’s start with shop 1.
Shop 1
Cartons are 70p from shop 1 and they have an offer where you get 20% off. We want to find the total cost and there are two different ways that we can do this. The first way is to find the total cost of the 12 cartons at full price, and then take the 20% off. The second method is to take 20% off of the price of one carton, and then multiply the sale price by the number of cartons (12).
I am going to use the first method. We find the cost of 12 cartons by multiplying 70p (the cost of 1 carton) by 12.
We now take 20% off. The easiest way to do this is to find out what 10% is, and then double it to find what 20% is. The full price represents 100% and we are able to find what 10% is by dividing by 10.
We want 20% so we multiply by 2.
We have found that 20% is £1.68. This is how much we get off of the full price of the 12 cartons. Therefore, we work out how much we pay by taking £1.68 off of £8.40. I am going to do this by using column subtraction and the working is shown below (click here if you would like to know more about column subtraction):
The cost of purchasing 12 cartons from shop 1 is £6.72.
Shop 2
Cartons from shop B are 80p and they have an offer whereby if you purchase three cartons, you get the 4th carton free. The best way to work out the cost of 12 cartons from this shop is to work out the cost of the cartons for one offer. We then multiply this cost by the number of times that we need to purchase the offer to have the desired quantity.
The offer from this shop involves 4 cartons. For the 4 cartons, you pay for 3 of them and you get the 4th carton free. Therefore, we can work out the cost of 4 cartons when on offer by multiplying the cartons that you pay for (3) by the cost for a carton (80p).
Shop 2
Cartons from shop B are 80p and they have an offer whereby if you purchase three cartons, you get the 4th carton free. The best way to work out the cost of 12 cartons from this shop is to work out the cost of the cartons for one offer. We then multiply this cost by the number of times that we need to purchase the offer to have the desired quantity.
The offer from this shop involves 4 cartons. For the 4 cartons, you pay for 3 of them and you get the 4th carton free. Therefore, we can work out the cost of 4 cartons when on offer by multiplying the cartons that you pay for (3) by the cost for a carton (80p).
The next step is to find out how many offers we need to purchase to have the desired quantity. The offer involves 4 cartons and we want to have 12 cartons. Therefore, we need to purchase 3 offers. We find out the total cost of 12 cartons by multiplying the cost of one offer (£2.40) by the number of offers needed (3).
12 cartons costs £7.20 from shop 2.
The final step is to compare the costs between the two shops; the cost from shop 1 was £6.72 and the cost from shop 2 was £7.20. This tells us that shop 1 is cheaper, thus meaning that I should purchase the 12 cartons from shop 1.
The final step is to compare the costs between the two shops; the cost from shop 1 was £6.72 and the cost from shop 2 was £7.20. This tells us that shop 1 is cheaper, thus meaning that I should purchase the 12 cartons from shop 1.
Example 2
You may use a calculator for the following question.
Two shops sell a candle and the non-sale price of the candle is the same from both shops. Each of the shops have a different offer on and the offers are shown below:
I want to purchase exactly 10 candles and I can purchase candles from both shops. What is the cheapest way of purchasing 10 candles?
There are two differences between this question and the other question. One of these differences is that we are not given the cost of the candles. The second difference is that we are now able to purchase candles from both of the shops.
We start answering the question by working out which shop is cheaper per candle when purchasing the full number of candles in the offer. As we are not given a price in the question, I am going to let the price of the candles be £1.
Shop A
The offer from shop A is "purchase 2 candles and get the next two candles half price". The first two candles will be full price, so both of these candles will be £1. The next two candles will be half price, which means that these two candles will be £0.50. The calculation below works out the cost for 4 candles.
You may use a calculator for the following question.
Two shops sell a candle and the non-sale price of the candle is the same from both shops. Each of the shops have a different offer on and the offers are shown below:
- Shop A: buy 2 candles and get the next two candles half price.
- Shop B: 20% off candles
I want to purchase exactly 10 candles and I can purchase candles from both shops. What is the cheapest way of purchasing 10 candles?
There are two differences between this question and the other question. One of these differences is that we are not given the cost of the candles. The second difference is that we are now able to purchase candles from both of the shops.
We start answering the question by working out which shop is cheaper per candle when purchasing the full number of candles in the offer. As we are not given a price in the question, I am going to let the price of the candles be £1.
Shop A
The offer from shop A is "purchase 2 candles and get the next two candles half price". The first two candles will be full price, so both of these candles will be £1. The next two candles will be half price, which means that these two candles will be £0.50. The calculation below works out the cost for 4 candles.
Therefore, the cost for 4 candles is £3. The next step is to find out the cost of each of the candles when on offer. We find the cost of each of the candles when on offer so that we can compare the cost of the candles from each of the shops. We find the cost of the candles when on offer by dividing the cost of the whole offer (£3) by the number of candles (4).
When the whole offer is purchased from shop A, the cost per candle is £0.75 (or 75p).
Shop B
We do the same for shop B. The offer from shop B is 20% off the candles. We said that the full price of the candle was £1 and 20% of £1 is £0.20. We find the sale price by taking £0.20 from £1.
Shop B
We do the same for shop B. The offer from shop B is 20% off the candles. We said that the full price of the candle was £1 and 20% of £1 is £0.20. We find the sale price by taking £0.20 from £1.
The offer price of each candle is £0.80 (or 80p).
Comparing
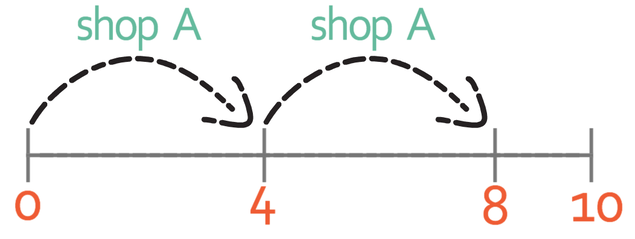
We are now able to compare the costs of the candles from each of the shops when purchased on offer. The cost of a candle from the first shop when purchased on offer is £0.75 and the cost of a candle when purchased on offer from the second shop is £0.80. We want to purchase the candles as cheaply as possible. Therefore, we want to purchase as many candles as possible on offer from shop A. In order to take advantage of the offer from shop A, we need to purchase 4 candles. I want to purchase 10 candles, which means that I am able to get two offers of 4 candles from shop A; this works out as 8 candles in total. The number line shows my purchasing pattern below.
Comparing
We are now able to compare the costs of the candles from each of the shops when purchased on offer. The cost of a candle from the first shop when purchased on offer is £0.75 and the cost of a candle when purchased on offer from the second shop is £0.80. We want to purchase the candles as cheaply as possible. Therefore, we want to purchase as many candles as possible on offer from shop A. In order to take advantage of the offer from shop A, we need to purchase 4 candles. I want to purchase 10 candles, which means that I am able to get two offers of 4 candles from shop A; this works out as 8 candles in total. The number line shows my purchasing pattern below.
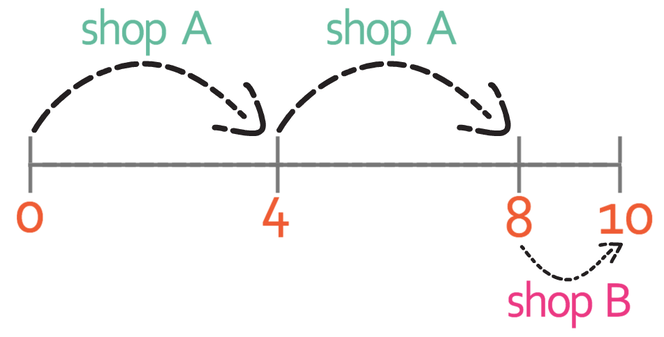
The final step is to purchase the remaining two candles. When I am unable to take advantage of the offer from shop A, the cost of each candle is £1. Therefore, it is cheaper for me to purchase the remaining 2 candles from shop B because £0.80 is less than/ cheaper than £1.
Therefore, the cheapest way to purchase 10 candles is to purchase 8 candles from shop A and 2 candles from shop B.