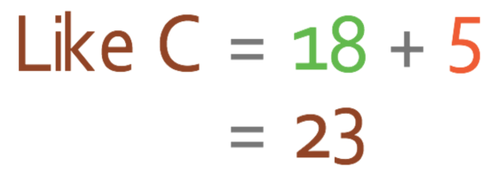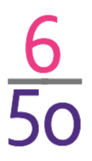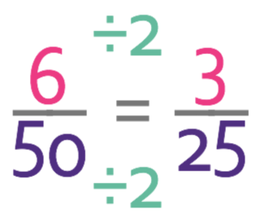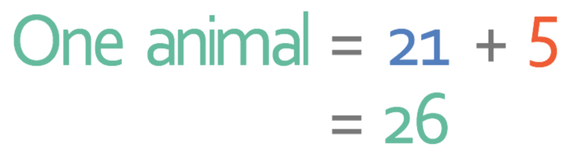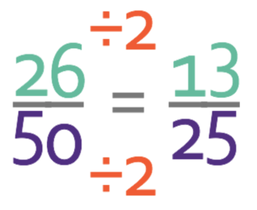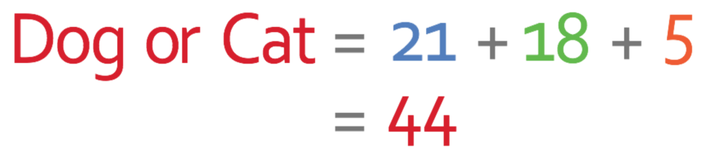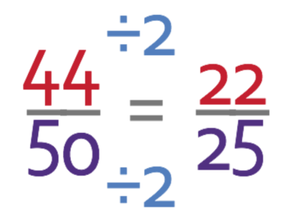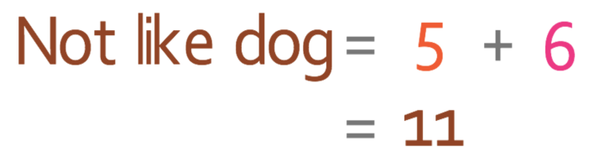Back to AQA Probability (H) Home
5 T) Venn Diagrams – Part 3: Probability
5 T) Venn Diagrams – Part 3: Probability
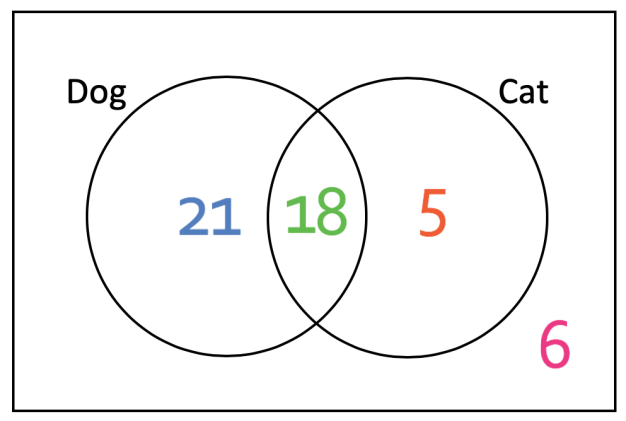
We are able to work probabilities of events happing from Venn diagrams. We are going to use the Venn diagram that we looked at in the previous section (click here to find more information about how this Venn diagram came about).
Question 1
I choose an individual at random. What is the probability that the individual that I choose likes cats?
We are able to find the number of individuals that like cats by finding the number of individuals that are inside the “like cats” circle. The “like cats” circle is made up of two different areas; the individuals who like cats and dogs (the centre of the Venn diagram) and of individuals that like cats and not dogs (the right part of the Venn diagram). There are 18 individuals who like cats and dogs, and 5 individuals that like cats and not dogs.
I choose an individual at random. What is the probability that the individual that I choose likes cats?
We are able to find the number of individuals that like cats by finding the number of individuals that are inside the “like cats” circle. The “like cats” circle is made up of two different areas; the individuals who like cats and dogs (the centre of the Venn diagram) and of individuals that like cats and not dogs (the right part of the Venn diagram). There are 18 individuals who like cats and dogs, and 5 individuals that like cats and not dogs.
Therefore, the number of individuals that like cats is 23 and there are 50 individuals in total. This means that the probability of choosing an individual that likes cats is:
There are no common factors between the numerator (23) and the denominator (50), which means that this fraction is in its simplest form.
Question 2
I randomly choose an individual. What is the probability that I choose an individual that does not like cats or dogs?
Individuals that do not like cats and do not like dogs will appear outside both the “like cats” and “like dogs” circle. There are 6 people outside both circles. This means that the probability is:
I randomly choose an individual. What is the probability that I choose an individual that does not like cats or dogs?
Individuals that do not like cats and do not like dogs will appear outside both the “like cats” and “like dogs” circle. There are 6 people outside both circles. This means that the probability is:
Both the numerator and the denominator are even, which means that they have a common factor of 2. Therefore, we divide both the numerator and the denominator by 2.
Therefore, the probability of choosing an individual that does not like cats and does not like dogs is 3/25.
Question 3
What is the probability that the individual that I choose likes exactly one of the animals?
There are two different cases whereby an individual like exactly one of the animals:
We add the number of individuals in these two sections together to find the total number of individuals that like exactly one of the animals.
What is the probability that the individual that I choose likes exactly one of the animals?
There are two different cases whereby an individual like exactly one of the animals:
- One case is whereby an individual likes dogs and not cats. This part is on the left of the diagram and there are 21 people in this section of the Venn diagram.
- The second case is whereby an individual likes cats and not dogs. This part is on the right of the Venn diagram and there are 5 people in this section of the Venn diagram.
We add the number of individuals in these two sections together to find the total number of individuals that like exactly one of the animals.
We now know that 26 individuals like exactly one of the animals. There are 50 people in total and this means that the probability of choosing an individual that like exactly one of the animals is:
Both the numerator and the denominator are even, which means that we can divide them both by 2.
Therefore, the probability of choosing an individual that likes exactly one of the animals is 13/25.
And & Or
Venn diagrams are very useful at finding out probabilities that look at “and” or “or”.
Question 4
I choose an individual at random. What is the probability that the individual that I choose likes both dogs and cats?
The area on the Venn diagram where people like both cats and dogs is where the two circles overlap one another. There are 18 individuals in this part of the diagram. There are 50 people in total, which means that the probability is:
Venn diagrams are very useful at finding out probabilities that look at “and” or “or”.
Question 4
I choose an individual at random. What is the probability that the individual that I choose likes both dogs and cats?
The area on the Venn diagram where people like both cats and dogs is where the two circles overlap one another. There are 18 individuals in this part of the diagram. There are 50 people in total, which means that the probability is:
This fraction can be simplified to become:
Sometimes you will see the and probability written with a ⋂; remember the n as meaning and. For example, the question could have been written like: P(D ⋂ C). We will be looking at this notation in more detail in part 5.
Question 5
Now, let’s find the probability that an individual chosen at random likes dogs or cats. There are three different ways that an individual can like dogs or cats. These three ways are:
We can add the number of individuals in each of these categories up to see how many individuals like cats or dogs. 18 people like dogs and cats, 21 people like dogs and do not like cats, and 5 people like cats and do not like dogs.
Now, let’s find the probability that an individual chosen at random likes dogs or cats. There are three different ways that an individual can like dogs or cats. These three ways are:
- They like dogs and cats
- They like dogs and do not like cats
- They like cats and do not like dogs
We can add the number of individuals in each of these categories up to see how many individuals like cats or dogs. 18 people like dogs and cats, 21 people like dogs and do not like cats, and 5 people like cats and do not like dogs.
This means that there are 44 people that like dogs or cats, meaning that the probability of choosing an individual that likes dogs or cats is:
This can be simplified down to:
The notation for asking or is a ∪. For example, for this question, the notation could have been: P(D ∪ C).
Question 6: Does Not Like
We are now going to find the probability of randomly choosing an individual that does not like dogs. We are able to do this in two ways.
The first way is to find the number of individuals that are outside of the “likes dog” circle, which includes the individuals who like cats and not dogs (5), and the individuals that do not like dogs and do not like cats (6).
We are now going to find the probability of randomly choosing an individual that does not like dogs. We are able to do this in two ways.
The first way is to find the number of individuals that are outside of the “likes dog” circle, which includes the individuals who like cats and not dogs (5), and the individuals that do not like dogs and do not like cats (6).
There are 11 individuals who do not like dogs, and this means that the probability of choosing an individual that does not like dogs is:
The second method of finding the number of individuals who do not like dogs is to take the number of individuals who do like dogs away from the total number of individuals that were asked. We are able to do this because liking dogs and not liking dogs are mutually exclusive events, which are events that cannot happen at the same time; you can’t like and not like dogs at the same time – you either like them, or you do not.
39 individuals like dogs (we obtain this number by adding the numbers that are inside the “like dogs” circle). There are 50 people that have been asked in total, so we minus 39 from 50, which tells us that there are 11 people that do not like dogs.
39 individuals like dogs (we obtain this number by adding the numbers that are inside the “like dogs” circle). There are 50 people that have been asked in total, so we minus 39 from 50, which tells us that there are 11 people that do not like dogs.
This means that the probability of choosing an individual that does not like dogs is:
This is exactly the same probability that we found out earlier.
There wasn’t much difference in the time taken to work out the probability by using either of these methods, but the second method will be quicker if there were 3 circles; for example, we introduced another animal, such as snakes.
When dealing with probability, you may see a ' and this means not. For example, suppose that we are to denote liking dogs as D. We could write P(D') to mean the probability of choosing an individual that does not like dogs.
There wasn’t much difference in the time taken to work out the probability by using either of these methods, but the second method will be quicker if there were 3 circles; for example, we introduced another animal, such as snakes.
When dealing with probability, you may see a ' and this means not. For example, suppose that we are to denote liking dogs as D. We could write P(D') to mean the probability of choosing an individual that does not like dogs.