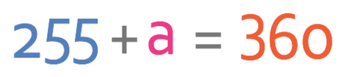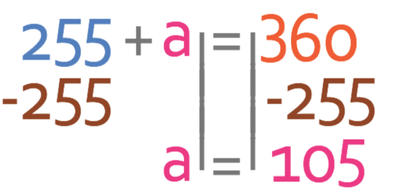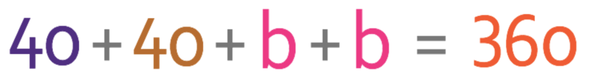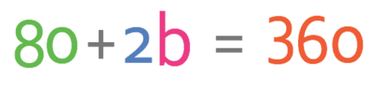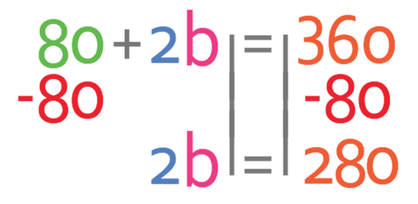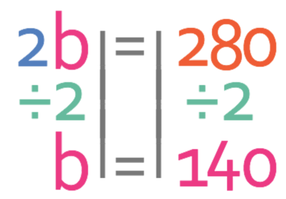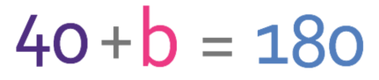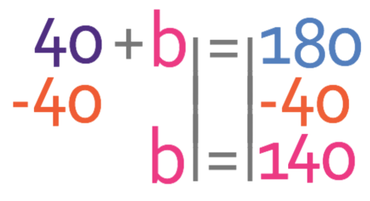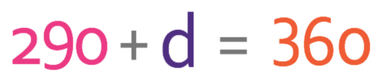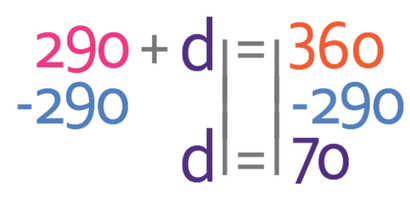Back to Edexcel Angles, Lines & Polygons (F) Home
4.1 C) Quadrilaterals – Part 2
4.1 C) Quadrilaterals – Part 2
The content in this section builds on the content that was discussed in the previous section. Therefore, make sure that you have covered the content in the previous section before working through the content in this section (click here to be taken to the previous section).
Example 1
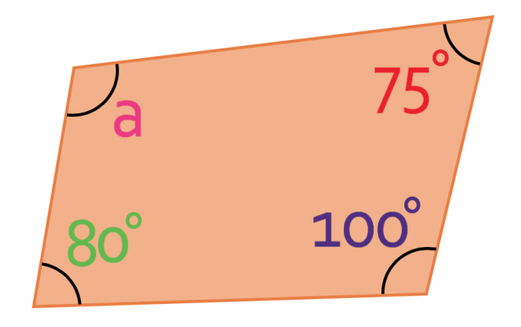
What is the size of angle a in the quadrilateral below?
What is the size of angle a in the quadrilateral below?
The first step to answering a question like this would be to identify what type of quadrilateral this is. However, we do not need to find out what type of quadrilateral the above quadrilateral is because we are given 3 of the 4 angles and we are asked to find out the size of the unknown angle. We know that the angles in a quadrilateral add up to 360°. Therefore, we can create the following equation:
The first step in finding the value for a is to collect all of the numbers that are on the left side of the equation.
We find the value of a by moving the 255 from the left side of the equation to the right. We are able to do this by taking 255 from both sides of the equation.
Therefore, angle a is 105°.
Example 2
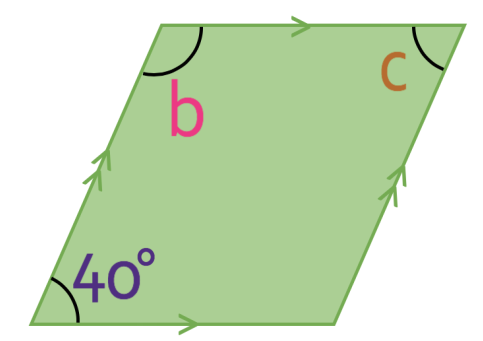
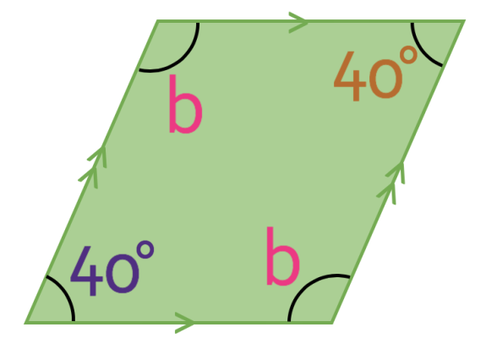
What is the value of b and c in the quadrilateral below?
What is the value of b and c in the quadrilateral below?
This quadrilateral is either a parallelogram of a rhombus. We are unable to determine which one of these it is because we are not given information about the lengths of the sides; we know that opposing sides in the above shape are of the same length and parallel to each other, but we do not know if all of the sides are the same length (all of the sides need to be the same length for the shape to be a rhombus). However, this does not matter because opposite angles in a rhombus and a parallelogram are the same size. This means that angle c is 40°. Also, angle b will be the same as the angle in the bottom right corner.
We are now able to find angle b because we know that all of the angles in a quadrilateral add up to 360°. This gives us the following equation:
The first step in finding the value of b is to collect like terms on the left side of the equation; we can collect the numbers and the unknowns.
We find the value of b by getting all of the terms that contain b to one side of the equation and all of the numbers to the other side of the equation. I am going to have all of the b’s on the left side of the equation and all of the numbers on the right. This means that I need to move the 80 that is currently on the left side to the right. I am able to do this by doing the opposite; I take 80 from both sides of the equation.
We want to find the value of b and not 2b. Therefore, we need to divide both sides of the equation by 2.
This tells us that b is 140°.
Alternative Method
We could have used another rule to find the value of b. The rule is that angles inside parallel lines add up to 180°. There are 4 pairs of angles in the above shape that are inside parallel lines and each of these pairs will add to 180°; these pairs of angles are top left & top right, top right & bottom right, bottom right & bottom left, and bottom left & top left).
We want to find the size of b, which is the top angle. We know that the bottom left angle and top left angle will add up to 180° because these two angles are inside parallel lines. Therefore, we can create the following equation.
Alternative Method
We could have used another rule to find the value of b. The rule is that angles inside parallel lines add up to 180°. There are 4 pairs of angles in the above shape that are inside parallel lines and each of these pairs will add to 180°; these pairs of angles are top left & top right, top right & bottom right, bottom right & bottom left, and bottom left & top left).
We want to find the size of b, which is the top angle. We know that the bottom left angle and top left angle will add up to 180° because these two angles are inside parallel lines. Therefore, we can create the following equation.
We find the value of b by moving the 40 from the left side of the equation to the right. We are able to move the 40 by taking 40 from both sides.
Therefore, b is 140° and this is the same answer as the previous method.
We will be looking at all of the rules to do with parallel lines in a later section.
We will be looking at all of the rules to do with parallel lines in a later section.
Example 3
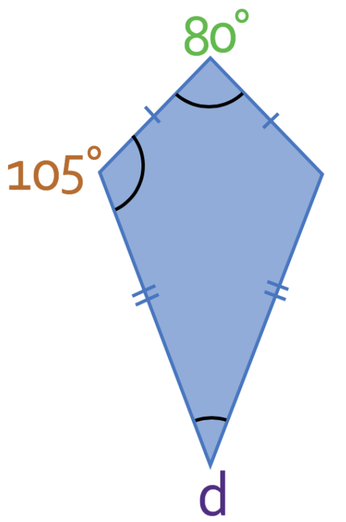
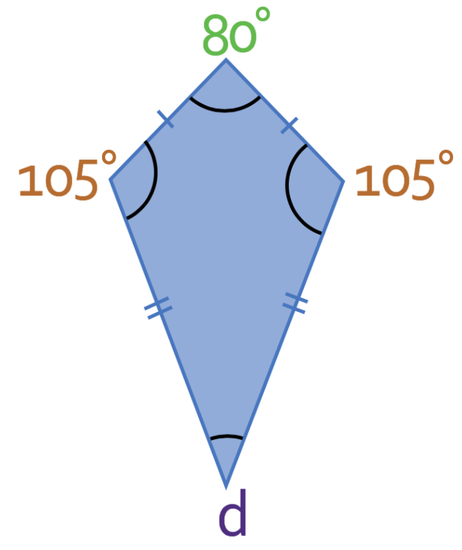
What is the size of angle d in the quadrilateral below?
What is the size of angle d in the quadrilateral below?
The quadrilateral above is a kite because there are two pairs of equal sides that are next to one another. This means that the two angles between the sides that are not of equal length will be the same. Therefore, the angle on the right will be 105°.
We are now able to work out the value of d because we have the size of 3 of the angles and we know that the sum of all 4 of the angles will add up to 360°. We can create the following equation from this information:
The first step in finding the value of d is to collect all of the numbers on the left side of the equation.
We want to find the value of d and we do this by moving the 290 from the left side of the equation to the right. We move the 290 by doing the opposite; we take 290 from both sides of the equation.
This tells us that d is 70°.