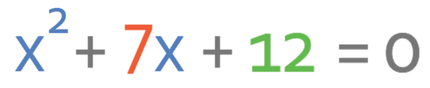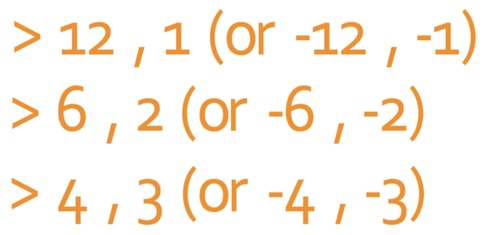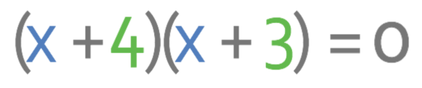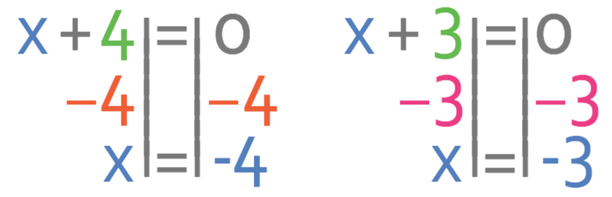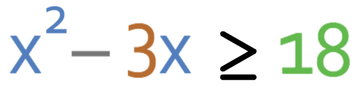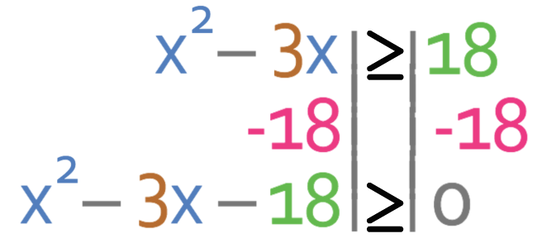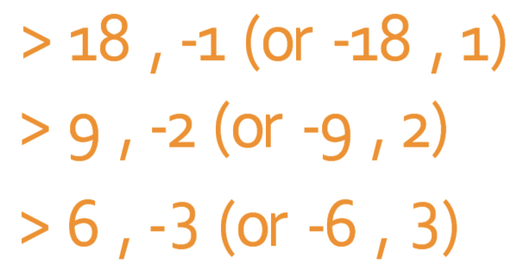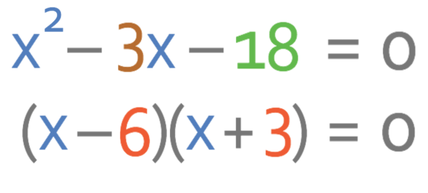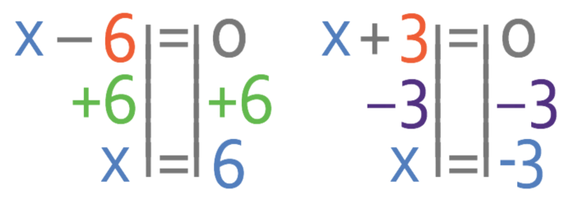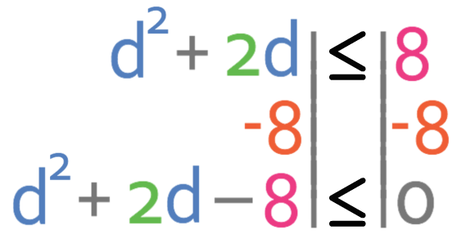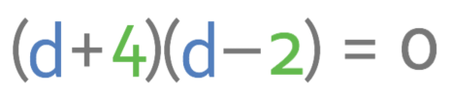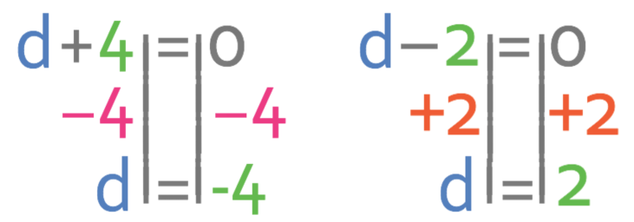Back to Edexcel Inequalities (H) Home
1.5 H) Solving Quadratic Inequalities – Part 2
The content in this section builds on the content that was discussed in the previous section. Make sure that you have covered the content in the previous section before working through the content in this section (click here to be taken to the content in the previous section).
Example 1
Solve the quadratic inequality.

The first step in answering this question is to find the roots for the quadratic. This quadratic has a square term (x2), a x term (7x) and a number (12). Therefore, we can solve the quadratic inequality by getting all of the terms to one side of the inequality, so that the other side of the inequality is 0. We then factorise. The quadratic inequality already has all of the terms on one side and 0 on the other side. Therefore, we can change the inequality sign to an equals sign, factorise and solve to find the roots.

​The coefficient of the square term is 1 (a is 1). This means that we factorise the quadratic by looking for two numbers that multiply to give 12 (the value of c) and add to give 7 (the value of b). The pairs of numbers that multiply to give 12 are shown below:
The only pair in the list above that adds to make 7 is 4 & 3. Therefore, our quadratic equation when factorised is:
We are now able to find the roots of the quadratic by letting each of the brackets equal 0.
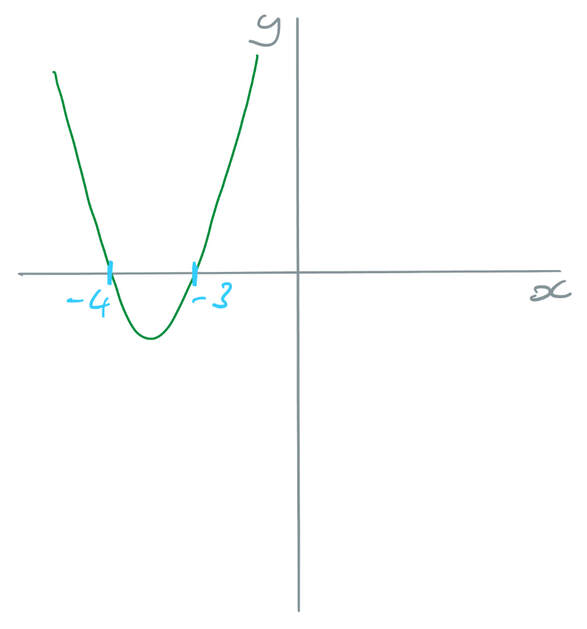
The roots for this quadratic are where x is -4 and -3. I am now going to sketch this graph and my sketch is given below.
The final step is to find where the curve satisfies the original inequality. The original inequality says that the quadratic is greater than zero. This means that we are looking for the values of x where the curve is above the x axis (where the curve has positive y values). There are two different parts where the curve is above the x axis and I have highlighted these on the graph below.
​There will be two different inequality solutions for this quadratic inequality because there are two different parts on the curve that satisfy the quadratic inequality. The solutions are:
Example 2
Solve the quadratic inequality.
​The first step in solving the inequality above is to get all of the terms to one side of the inequality, so that the other side of the inequality is zero. We get all of the terms to the side that has the most quadratic terms, which is the left side. We do this by moving the 18 from the right side of the inequality to the left. We are able to do this by taking 18 from both sides of the inequality.
​The next step is to change the inequality sign to an equals sign and factorise. The coefficient of the square term is 1 (a is 1). This means that we factorise by looking for two numbers that multiply together to give -18 (the value of c) and add together to make -3 (the value of b). As we are looking for two number that multiply to make a negative (-18), it means that we are going to have one positive number and a negative number. The pairs of numbers that multiply to give -18 are given below:
The only pair of numbers that add together to give -3 is -6 and 3. The factorised quadratic becomes.
We find the roots for the quadratic by letting each of the two brackets equal zero.
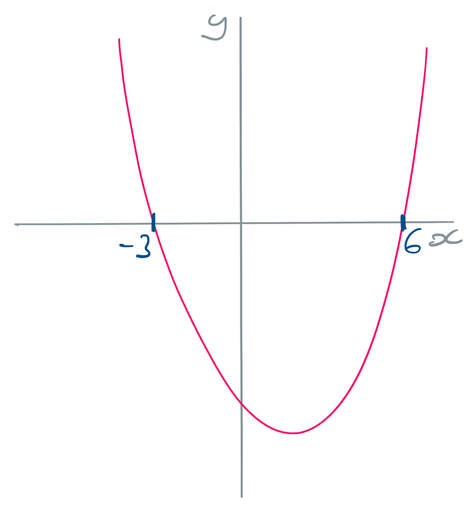
​Therefore, the roots of this quadratic are where x is 6 and -3. We are now able to sketch the curve.
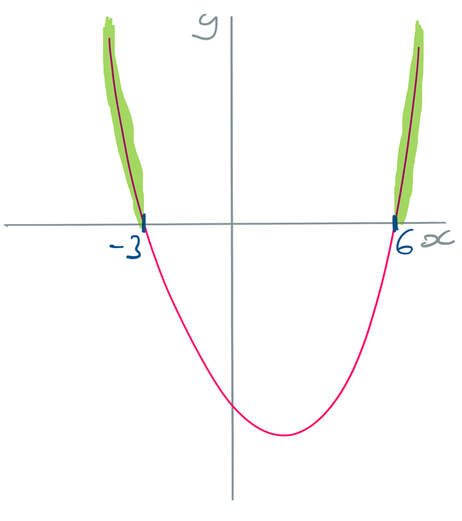
The inequality states that the quadratic is greater than or equal to zero. This means that we are looking for the x values where the curve is above or on the x axis. There are two different parts of the curve where this is the case and I have highlighted these on the graph below.
​The final step is to write inequalities that describe these two highlighted sections. The inequalities are:
Example 3
In the previous examples in this section and the section before, the unknowns have been x. We are now going to have a look at a question whereby the unknown is not x. We answer these questions in pretty much the same way; we find the roots for the unknown that we are given, and then we sketch the curve with the x axis being the axis for the unknown that we are working with. For example, if the variable in the inequality was d, the x axis would become the d axis.
 
Solve the quadratic inequality.
There are three different types of terms in this inequality; we have a square term, a linear term and a number. Therefore, we find the roots for the quadratic by getting all of the terms to one side of the inequality and then we factorise. It is always easier to factorise with a positive number of quadratic terms. Therefore, I am going to get all of the terms to the left side of the inequality. In order to achieve this, we need to move the 8 from the right side to the left; we can do this by taking 8 from both sides of the inequality.
The next step is to change the inequality sign to an equals sign.
The coefficient of the square term is 1 (a is 1). This means that we factorise this quadratic by looking for two numbers that multiply to give -8 (the value of c) and add to give 2 (the value of b). Here are the pairs of numbers that multiply to give -8:
The only one of these pairs that adds to give 2 is 4 and -2. Therefore, the factorised quadratic is.
We now find the roots by letting each of the brackets equal 0.
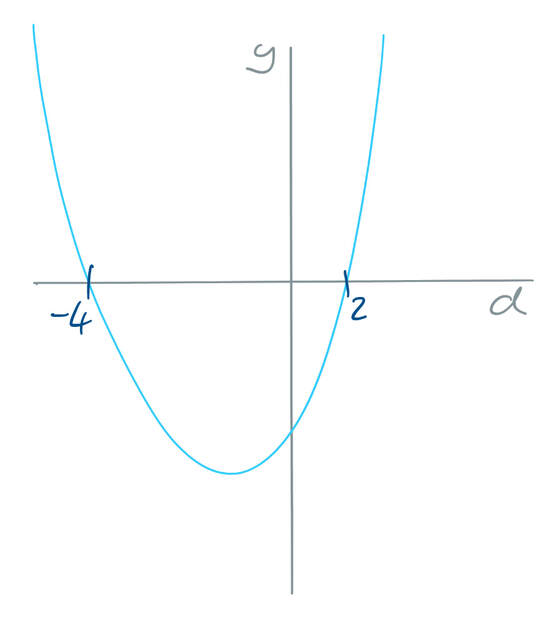
​This tells us that the roots for the quadratic are where d is -4 and 2. We are now able to sketch the quadratic. We are working with the unknown d and not x. This means that the x axis will be the d axis. My sketch of the quadratic is shown below.
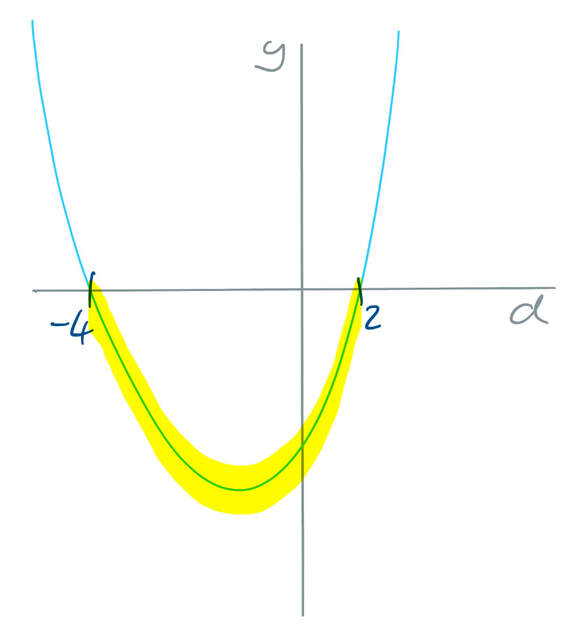
The inequality states that the quadratic is less than or equal to zero. This means that we are looking for the values of d whereby the curve is below the d axis or on the d axis. There is one part of the curve where this is the case and I have highlighted it on the graph below.
​The final step is to write an inequality to describe the highlighted part of the curve. The inequality is: