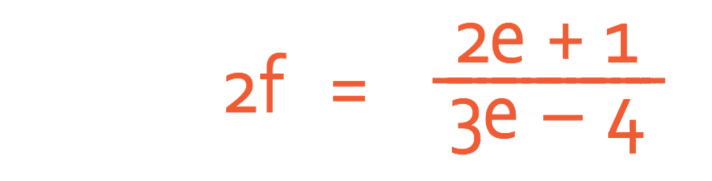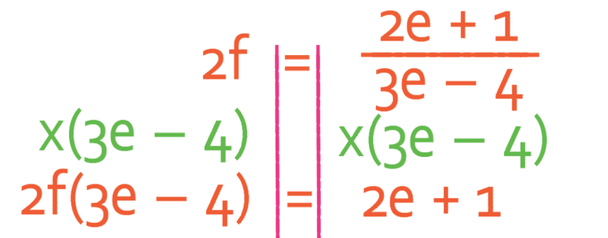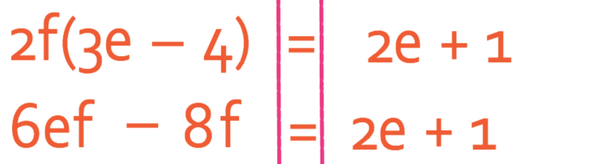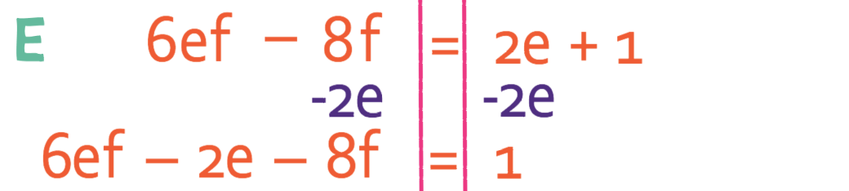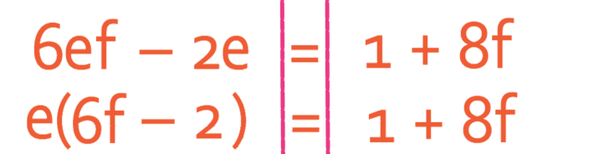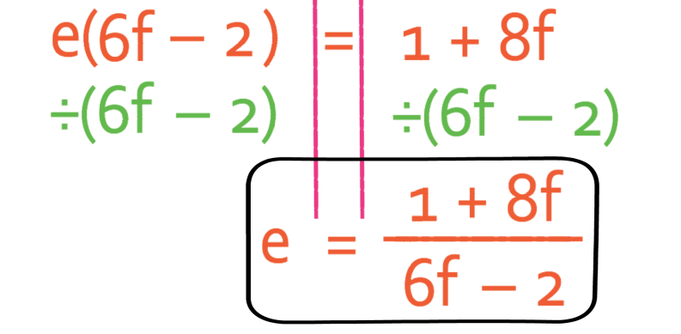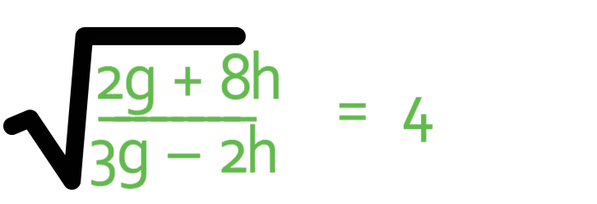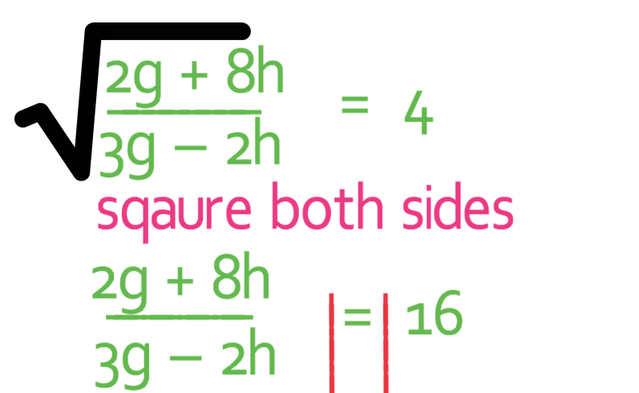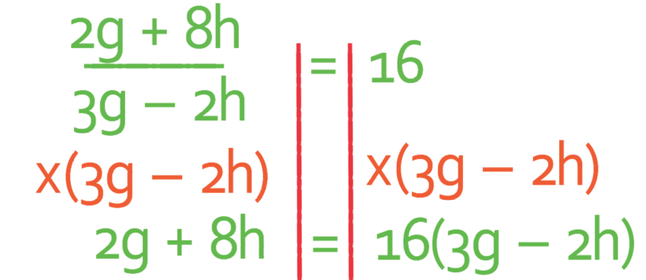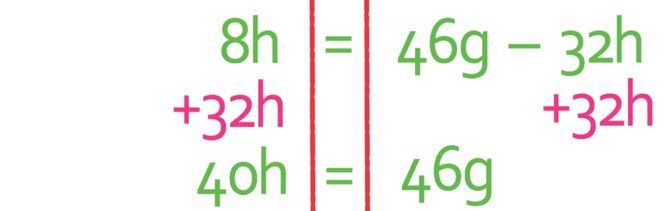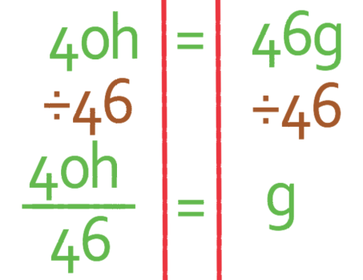Back to Edexcel Algebraic Formulae (H) Home
2.3 E) Rearranging Formulas – Part 2
2.3 E) Rearranging Formulas – Part 2
The examples in this section build on what has been discussed in the previous sections; make sure that you have gone through both of those sections before working your way through this section (click here to be taken through to part 1 and click here to be taken through to part 2).
Example 1
Make e the subject of the formula below.
Make e the subject of the formula below.
To make e the subject of the formula, we need to get all of the terms in the formula that have an e in them to one side of the formula and all of the other terms that do not have an e in them to the other side of the formula. However, we first need to find out what terms contain e and what terms do not contain e. We do this by getting rid of the denominator on the right side of the formula , which we do by multiplying both sides of the formula by the denominator, which is 3e – 4.
The next step is to expand the bracket out.
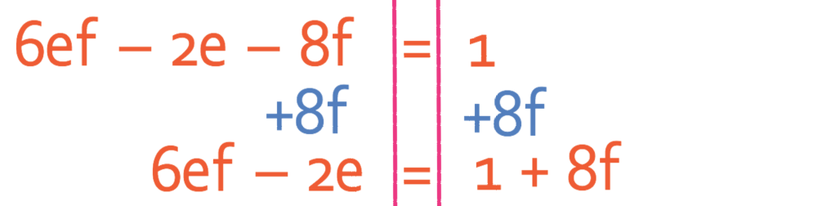
We now need to get all of the terms with an e on one side and all of the terms without an e on the other side of the formula. I am going to get all of my terms with an e to the left side of the formula, which means that I need to get the 2e that is currently on the right to the left. We do this by doing the opposite, which means that we take 2e from both sides of the formula.
The term -8f does not contain any e’s, which means that we need to move it from the left side of the formula to the right. We do this by adding 8f to both sides of the formula.
We now have all of the terms that contain e on the left side of the formula and all of the terms that do not contain e on the right side of the formula. This means that we are now ready to factorise out the e on the left side of the formula.
The next step is to divide both sides of the formula by the bracket; we divide both sides by 6f – 2.
We now have e as the subject of the formula.
Example 2
Make g the subject of the formula below.
Make g the subject of the formula below.
The first step for this question is to get all of the individual terms by themselves. The left side of the formula is a square root and square roots are fairly tricky to deal with. Therefore, to make the formula easier to deal with, we can get rid of the square root by squaring both sides of the formula; squaring both sides of the formula means multiplying each side of the formula by itself.
We now have a formula that is very similar to example 1 in the sense that we have a fraction on one side of the formula. We are able to get rid of our fraction by multiplying both sides of the formula by the denominator of the fraction, which is 3g – 2h.
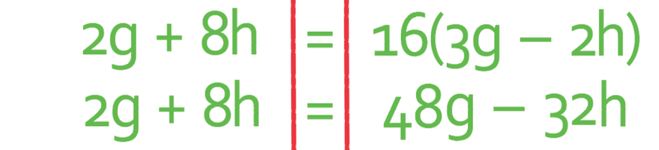
We now expand the right side of the formula.
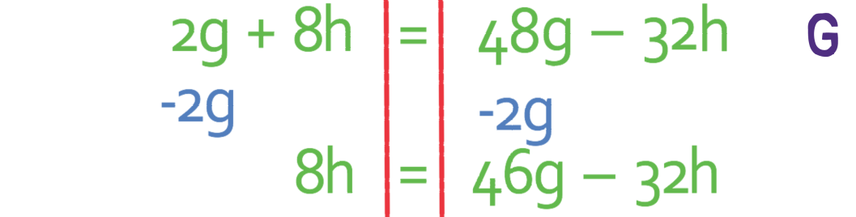
We are making g the subject, so we need to get all of the terms with g in them to the one side and all of the terms without g in them to the other side. I am going to get all of the terms with g to the right and all of the terms without g to the left. This means that I need to move the 2g that is currently on the left to the right, which we can do by taking 2g from both sides of the formula.
Also, I need to get the -32h to the left side of the formula because there is no g in it meaning that it should not be on the right side of the formula. I move it across by adding 32h to both sides of the formula.
There is only one term for g on the right side, which means that we can divide both sides of our formula by the number of g’s that there are; we divide both sides of the formula by 46 (there is no need to factorise when we only have one term that has the unknown that we are making the subject).
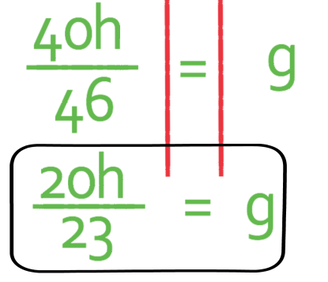
The final step is to make sure that we have given the fraction in its simplest form. We check that we have by looking for any common factors in the numerator and the denominator of the fraction, We then divide by any common factors that we find. The only common factor between the numerator and the denominator is 2, thus meaning that we divide the numerator and the denominator by 2.
We now have g as the subject of the formula.