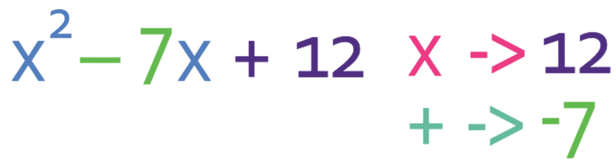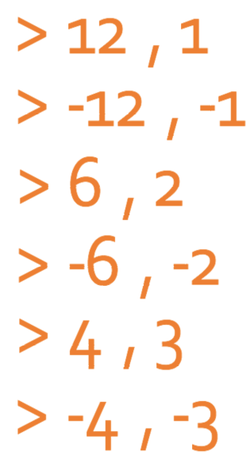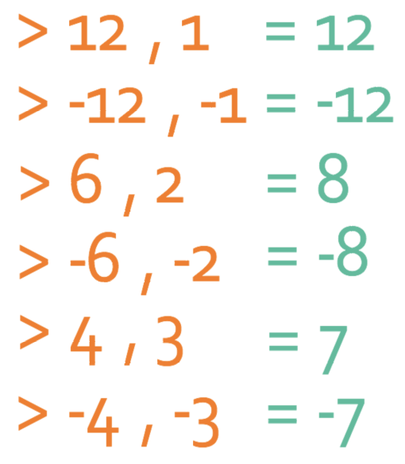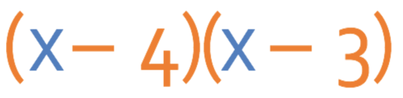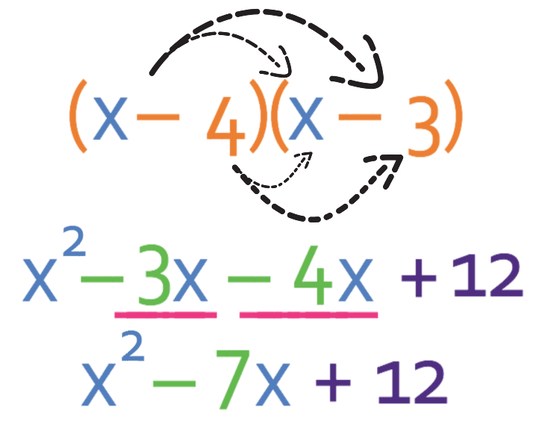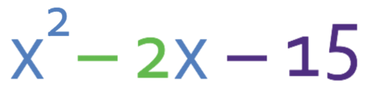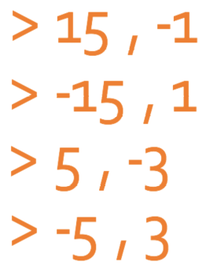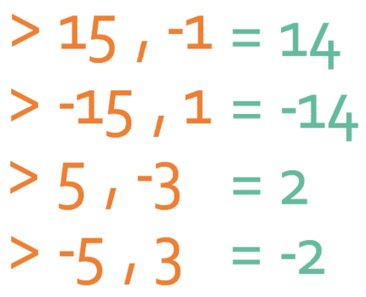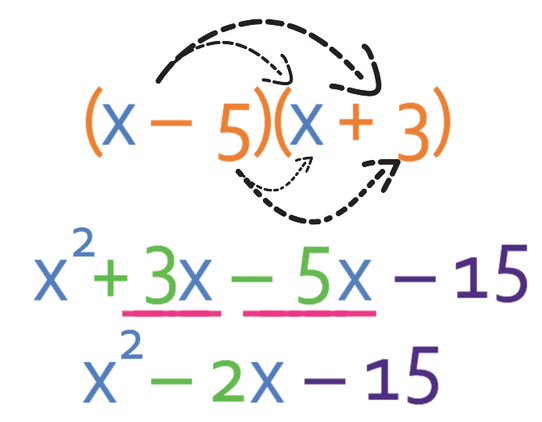Back to OCR Quadratic Equations: Factorising (F) Home
2.6 B) Factorising Quadratics (A = 1) – Part 2
2.6 B) Factorising Quadratics (A = 1) – Part 2
The content in this section builds on the content that was discussed in the previous section. Make sure that you have covered the content in the previous section before working through this section (click here to be taken to the previous section).
Example 1
Factorise the following quadratic equation:
Factorise the following quadratic equation:
a in this quadratic equation is 1, b is -7 and c is 12. As the value for a is 1, it means that there are two brackets with one x in each of them; the factorised brackets will be in the form (x + ?)(x + ?). To find the values of the question marks in the brackets, we are looking for two numbers that multiply together to give us 12 (the value of c), and add together to give -7 (the value of b).
Here are the pairs of numbers that multiply together to give 12:
We now check to see which pair adds together to give -7.
The only pair of numbers that add together to give -7 is the pair -4 and -3. Therefore, our factorised brackets are:
The order that the numbers are placed in the brackets does not matter; the answer could have been written as (x – 3)(x – 4).
We can check our answer by expanding the brackets and checking that we get the expression that we were factorising.
We can check our answer by expanding the brackets and checking that we get the expression that we were factorising.
This is the expression that we were factorising, thus meaning that we have factorised correctly.
Example 2
Factorise the expression below:
Factorise the expression below:
The value of a in the expression above is 1, b is -2 and c is -15. As the value for a is 1, it means that we are looking for two numbers that multiply together to give -15 (the value of c) and add together to give -2 (the value of b).
As the value of c is negative (-15), one of the numbers in the pair will be positive and the other number will be negative (the only way that we can obtain a negative is by multiplying a positive by a negative). Here are the pairs of number that multiply to give -15:
We now check to see which of the pairs add together to give -2.
-5 and 3 add together to make -2. Therefore, the factorised equation becomes:
Let’s just expand the brackets to check that we have factorised correctly.
The expanded brackets is the same expression that we were factorising, which means that we have factorised correctly.
Final Note
Whilst you are getting used to factorising and learning the technique, it is a good idea to write the pairs of numbers out. But whenever you become more confident with factorising, you probably won’t need to write the pairs of numbers out and will be able to find the numbers that you need inside the bracket in your head.
Whilst you are getting used to factorising and learning the technique, it is a good idea to write the pairs of numbers out. But whenever you become more confident with factorising, you probably won’t need to write the pairs of numbers out and will be able to find the numbers that you need inside the bracket in your head.